Информация и информационные процессы

Рефераты >> Коммуникации и связь >> Информация и информационные процессы

обозначается

Конъюнкция

Легко видеть, что логическая функция И совпадает с произведением аргументов. Поэтому её называют также логическим умножением. Ещё одно название¾Конъюнкция. Нетрудно определить функцию И для любого конечного числа аргументов. Она равна 1 тогда и только тогда, когда все сомножители равны 1, как и должно быть для произведения. Логическое умножение подчиняется переместительному и сочетательному законам.

-2+3=3+2 Коммутативны 7-3=3-7 Не коммутативны

7*3=3*7

(3+2)+7=3+(2+7)

5+7=3+9

(3*7)*2=3*(7*2)

И

Логическая функция ИЛИ

Логическая функция ИЛИ от двух аргументов определяется таблицей. Её называют логическим сложением или Дизъюнкцией. Следует помнить, что логическая сумма отличается от арифметической суммы. Логическая сумма нескольких слагаемых ровна 0 тогда и только тогда, когда все слагаемые равны 0. Эта операция также подчиняется переместительному и сочетательному законам.

Дизъюнкция

10

Логическая функция НЕ.

Логическая функция НЕ (отрицание) зависит от одного аргумента и определяется таблицей. Функция НЕ обозначается горизонтальной чертой над аргументом или особым знаком.

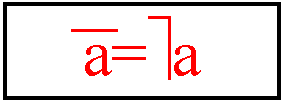Логические выражения и их образование.

Подобно арифметическим операциям, логические операции имеют различное «Старшинство», что отражается на порядке их выполнения в выражениях, содержащих символы различных операций: прежде всего выполняются операции НЕ, затем И и только потом ИЛИ. Здесь наблюдается полная аналогия с алгебраическими выражениями. При вычислении по формуле а2*b2+c2 сначала выполняется возведение в степень, затем умножение и тол ько потом сложение аналогично формуле.

Сначала выполняются отрицания, затем конъюнкция, а потом дизъюнкция. В тех случаях, когда нужно изменить этот порядок применяются круглые скобки. Правила их применения ничем не отличаются от правил применения скобок в алгебраической формуле.

Логические выражения и их преобразование.

Любую функцию трёх и более аргументов можно представить формулой, в которой в которой фигурируют элементарные логические функции. Например, функция три аргумента представленная таблицей.