где — корни характеристического уравнения

(2.18)

где Bi = aw/l — критерий Био.

Уравнение (2.18) имеет бесчисленное множество действительных положительных корней. Первые пять корней для различных значений критерия Био были вычислены Карслоу и Егером. Обычно на практике пользуются номограммами. Номограмма позволяющая определить безразмерную температуру при различных значениях критерях Био приведена на рис.2.3

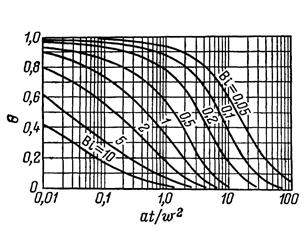
Рис. 2.3 Номограмма для определения безразмерной температуры поверхности неограниченной пластины.

Ана­логичная номограмма, предназ­наченная для определения тем­пературы в центре пластины, при­ведена на рис.2.4.

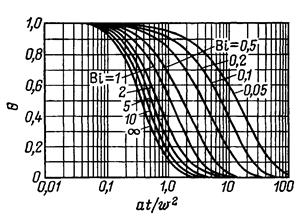
Рис. 2.4 Номограмма для определения безразмерной температуры в середине неограниченной пластины

2.2.2 Неограниченный цилиндр.

Рас­смотрим неограниченный цилиндр радиуса R, температура поверх­ности которого остается неизмен­ной на протяжении всего процес­са теплообмена. Радиальное рас­пределение температур в началь­ный момент задано в виде некоторой функции Т(r). Необходимо найти распределение температур определения в цилиндре в любой момент времени. Задачи такого типа встречаются при расчете процессов охлаждения полимерного волокна, затвердевания литников литьевых форм и т. п.

Дифференциальное уравнение теплопроводности для цилиндра

имеет вид: 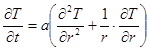(2.19)

Краевые условия:

Решение, полученное методом разделения переменных, в без­размерной форме, имеет вид:

(2.20)

Для оценки изменения теплосодержания цилиндра определим среднюю температуру как:

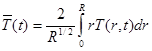(2.21)

Тогда безразмерная средняя температура определится соотноше­нием: (2.22)

где ; - корни функции Бесселя первого рода нулевого порядка определяемые выражением:

(2.23)

Таким образом, уменьшение средней температуры описывается простым экспоненциальным законом. Для удобства прикидочных расчетов на рис. IV. 10 приведена номограмма зависимости между q и Fo.

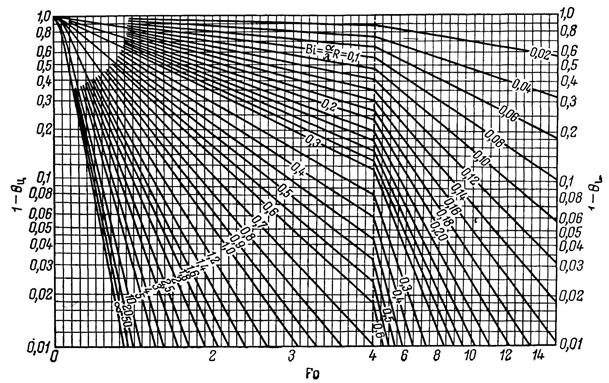
Рис. 2.5 Номограмма для определения зависимости между безразмерной средней избы­точной температурой и критерием Фурье в случае неограниченного цилиндра.

2.3. Теплопроводность в процессах, сопровождающихся изменением физического состояния

Анализируя процессы переработки полимеров, часто приходится встречаться с задачей о нагреве или охлаждении полимера, сопровождающемся изменением физического состояния (плавлением или затвердением). Теоретическое рассмотрение задач такого типа впервые выполнено Нейманном.

Мы остановимся только на одном, наиболее простом случае, в котором для упрощения теплофизические характеристики расплава и твердого полимера будем считать одинаковыми. Пусть скрытая теплота плавления равна λ, а температура плавления Тп. Обозначим координату поверхности раздела между твердой и жидкой фазами через Х(t). Тогда одно из граничных условий которое должно удовлетворяться на этой поверхности, запишется в виде:

Ts = Tm = Tn при X=X(t) (2.24)

Индекс s указывает, что соответствующая величина относится к твердой фазе (например, ρs — плотность твердой фазы). Соответственно индекс m указывает, что величина относится к жидкой фазе.

Второе граничное условие касается поглощения (или выделения) скрытой теплоты на поверхности раздела. Предположим, что в области x>x(t) находится жидкость при температуре Тт(х, t), а в области x=x(t) — твердая фаза при температуре Ts(xtt).

Если поверхность раздела перемещается на расстояние dx, то в элементе объема вещества выделяется и должно быть отведено в результате теплопроводности количество тепла, в пересчете на единицу поверхности равное lρdx. Математически это условие за­пишется в виде:

(2.25)

Рассмотрим три случая: плавление, затвердевание и плавление с удалением расплава.

2.3.1. Плавление в области х > 0.

Если в начальный момент область х > 0 занята твердым телом с постоянной температурой Ts0 и при t > 0 плоскость х = 0 поддерживается при постоянной темпера­туре Т2 > Тп, то положение плоскости плавления определится вы­ражением:

(2.26)

Здесь - корень уравнения

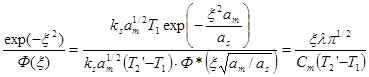(2.27)

где

;

При этом распределение температур в твёрдой и жидкой фазах описывается выражением:

(2.28)

(2.29)

2.3.2. Затвердевание.

Пусть в начальный момент времени область х > 0 представляет собой жидкость, а область х <С 0 — твердое тело. Иначе говоря, в начальный момент поверхность раздела сов­падает с началом координат.

Допустим, что значения термических коэффициентов только что затвердевшего расплава отличаются от значений термических коэффициентов твердой фазы вобласти х < 0. Присвоим термиче­ским коэффициентам этой области индекс s0.

Поступающий расплав имеет температуру Т2. Координата по­верхности раздела фаз определится соотношением:

(2.30)

Здесь ξ — корень уравнения

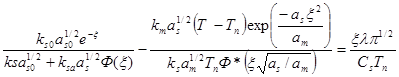(2.31)

После определения ξ, которое может быть выполнено любым численным методом (например, методом итерации), можно опре­делить температурные поля во всех трех областях (начальная твердая фаза, затвердевшее вещество и расплав):

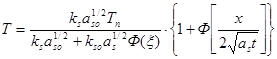(2.34)

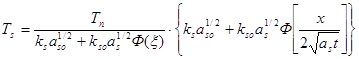(2.35)

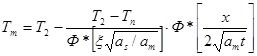(2.35)

2.3.3 Плавление с непрерывным удалением расплава.

Пусть твердое тело нагревается благодаря поступающему извне к его поверхно­сти постоянному тепловому потоку q. При этом весь расплав не­прерывно удаляется. Примем плоскость, на которой происходит плавление, за плоскость с координатой х = 0 и будем считать, что твердое тело в области х > 0 движется относительно этой плос­кости со скоростью υ. Следовательно, массовый расход расплава, Qm, отнесенный к единичной ширине, равен: