Определение 2. Матричным представлением группы G называется гомоморфизм этой группы в группу невырожденных комплексных или действительных матриц размера n´n.

Определение 3. Подстановочным представлением группы G называется гомоморфизм этой группы в группу подстановок порядка n. Если гомоморфизм группы G в группу операторов, матриц или подстановок является изморфизмом, то он называется точным представлением.

Представление группы будем обозначать буквой Т. Пусть g1 и g2 – любые элементы группы G, а Т(g1) и Т(g2) – соответствующие этим элементам матрицы представления. Тогда согласно определению гомоморфизма группы

Т(g1, g2)= Т(g1) Т(g2). (4)

Определение 4. Два матричных представления Т1 и Т2 группы G в некоторую группу матриц называется эквивалентным, если существует невырожденная матрица F такая, что для всех матриц Т1(g), Т2(g) представления будет иметь место равенство

Т2(g)=Ф-1 Т1(g)Ф, "gÎG (5)

Эквивалентные представления не различаются.

2. Приводимые и неприводимые представления

Воспользуемся языком линейных операторов. Пусть дано некоторое представление Т группы G, действующее в векторном пространстве V. Каждому вектору vÎV оператор (g)ºсопоставляет вектор (v)=v1 этого же пространства. Пусть W – подпространство пространства V.

Определение 5. Подпространство W пространства V называется инвариантным подпространством действия , если, каковы бы ни были элементы gÎG и векторы wÎW, T(w)=w1, где w1ÎW.

Определение 6. Представление T группы G, действующее в векторном пространстве V над полем Р, называется приводимым представлением, если в этом пространстве существуют неприводимые инвариантные относительно этого действия подпространства. Представление Т называется неприводимым, если единственные его инвариантные подпространства – О и само пространство V.

Интерпретируем это определение на языке матриц. Пусть представление Т группы G приводимо. Значит, в пространстве V представления может быть найдено нетривиальное инвариантное подпространство W. Пусть e1, e2, …, ek – базис пространства W. Дополним его до базиса е1, е2, …, еk, ek+1, …, en всего пространства V. Так как W инвариантно, то (еi), где i=1, 2, …, k лежат в W. Поэтому

(еi)=a1ie1+a2ie2+…+akiek, i=1, 2, …, k.

Но так как эти векторы лежат и в пространстве V, то можно также написать

(еi)=a1ie1+a2ie2+…+akiek+0ek+1+…+0en, i=1, 2, …, k.

Что же касается отдельных базисных векторов ek+1, ek+2, …, en, то, поскольку они не принадлежат W, их образы выражаются через базис наиболее общим способом и получаем следующую картину:

(е1)=a11e1+a21e2+…+ak1ek+0ek+1+…+0en

(е2)=a12e1+a22e2+…+ak2ek+0ek+1+…+0en

(еk)=a1ke1+a2ke2+…+akkek+0ek+1+…+0en

(еk+1)=a1,k+1e1+a2,k+1e2+…+ak,k+1ek+ ak+1,k+1ek+1+…+an,k+1en

(еn)=a1ne1+a2ne2+…+aknek+ ak+1,nek+1+…+annen.

Отсюда видно, что матрицы всех элементов группы G в предствлении Т будут одновременно иметь следующий вид:

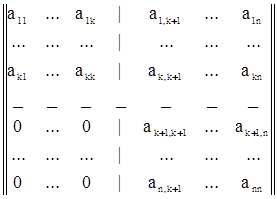(6)

Поэтому на языке матриц матричное представление называется приводимым, если все матрицы его могут быть записаны при определенном выборе базиса в виде (6). Если же ни при каком выборе базиса матрицы представления нельзя записать в указанном виде, представления называются неприводимыми.

3. Представления групп и модули

Рассмотрим конструкцию, позволяющую, зная представления групп, построить модуль М над кольцом K, связанный с этим представлением. Пусть теория представлений групп сформулирована на языке матриц и линейных операторов. Все матрицы данного порядка (линейные операторы в n-мерном пространстве) образуют относительно операций сложения и умножения матриц (линейных операторов) кольцо. Матрицы (линейные операторы) образуют алгебру в смысле следующего определения.

Определение 7. Алгеброй А над полем Р называется множество, в котором введены операции сложения и умножения элементов, а также операция умножения lаÎА, lÎР, аÎА элементов поля Р на элементы из А, причем: 1) относительно операций сложения и умножения А является кольцом; 2) относительно операций сложения и умножения на элементы поля Р алгебра является векторным пространством; 3) операции умножения элементов кольца и умножения на элементы из поля связаны аксиомой

l(ab)=(la)b=a(lb); lÎP; a, bÎA (7)

Матрицы, которые сопоставляются элементами группы в представлении Т, составляют лишь часть из множества всех матриц Мn, что следует хотя бы из того, что они невырождены. Однако, если Т(g1), Т(g2), …, T(gs), s=|G| - все матрицы представления группы G, то с ними можем связать алгебру, состоящую из всевозможных линейных комбинаций этих матриц вида

K=a1 Т(g1)+a2 Т(g2)+ +asT(gs); aiÎR или С (8)

Пусть Р – поле комплексных или вещественных чисел. Рассмотрим формальные суммы вида

a=a1g1+a2g2+…+angn; aiÎP; giÎG; i=1, 2, …, n; n=|G| (9)

Подчеркнем, что так как в группе G есть только одна операция – умножение, левую часть нельзя рассчитывать как результат сложения элементов правой части. Назовем две суммы 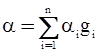и 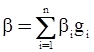равными, если ai=bi. Введем операцию сложения формальных сумм по правилу:

a+b=(a1+b1)g1+(a2+b2)g2+…+(an+bn)gn=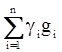; gi=ai+bi.

Видим, что на множестве формальных сумм определена операция сложения, так как в результате операции снова получилась формальная сумма вида (9). Введем далее операцию умножения формальных сумм. Получим кольцо, которое называется групповым кольцом группы G над полем Р и обозначается в виде PG. Это кольцо можно превратить в алгебру. Для этого надо определить умножение lÎP на aÎPG. Умножение задается по формуле

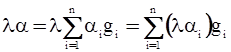. (10)

Относительно сложения и умножения по этой формуле PG представляет собой векторное пространство (аксиома (7)). Построенная алгебра называется групповой алгеброй группы G и обозначается, как и групповое кольцо, в виде PG.

Если сопоставить каждому элементу gi в выражении (9) матрицу T(gi) этого элемента в представлении Т, то получим матрицу (8), которую обозначим буквой K, так как она является элементом группового кольца матриц K. Как следует из определения модуля, главное при построении модуля – ввести умножение векторов на элементы группового кольца. Пусть V – пространство представления Т группы G. Произвольный вектор v этого пространства зададим координатами. Если А – матрица линейного оператора , действующего в векторном пространстве, то можно получить вектор v1, в который переходит вектор v под действием оператора . Для этого надо просто умножить по правилу умножения матриц вектор v на матрицу А. Аналогично выполняется умножение вектора v на элемент a группового кольца (и алгебры) PG: