2. Таблицы характеров неприводимых представлений

Приведенные свойства характеров позволяют описать построение таблиц характеров неприводимых представлений. Строки таблицы будем нумеровать, как принято в теории представлений групп характерами, но одновременно будем указывать обозначения, принятые в молекулярной спектроскопии и кристаллографии: одномерные представления обозначаются A1, B1, A2, B2, …, двумерные – E1, E2, … и, наконец, трехмерные – F1, F2, … .

Так как по свойству 2 характеры постоянны на каждом классе сопряженных элементов, то столбцы таблицы нумеруются классами сопряженных элементов. Под обозначением класса сопряженных элементов указывается число элементов в классе – порядок класса. Рассмотрим в качестве примера группу C3V. Классы сопряженных элементов группы C3V имеют вид K1={I}, K2={C3, C32}, K3={, , }. Известно, что группа C3V имеет три неприводимых представления, характеры которых приведены в табл. 2.

Таблица 2.

3. Разложение характеров по неприводимым представлениям

В соответствии с рассмотренными свойствами характер приводимого представления cT можно представить в виде разложения по характерам неприводимых представлений :

,

где ni – число, показывающее, сколько раз характер неприводимого представления Ti содержится в характере приводимого представления Т. На основании свойств ортогональности это число легко определяется, а именно:

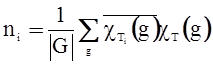. (19)

Формула (19) имеет важные применения в теории молекулярных спектров для определения числа состояний данного типа симметрии.

4. Определение характеров неприводимых представлений при применении групповых алгебр групп

Для достаточно широкого класса групп желательно иметь общий метод нахождения характеров неприводимых представлений.

Пусть дана группа G. Найдем классы сопряженных элементов Ki группы и обозначим сумму элементов группы, принадлежащих классу Ki. Здесь Сi являются элементами групповой алгебры PG группы G над полем Р. Проверим, перестановочны ли элементы Сi со всеми элементами алгебры PG. Для этого достаточно проверить, что для всех gÎG справедливы равенства gСi=Сig или Сi=g-1Сig.

Действительно,

g-1 Сig=g-1(k1+k2+…)g=g-1k1g+g-1k2g+…

Так как в групповой алгебре выполним дистрибутивный закон, то очевидно, что правая часть содержит все элементы Сi и, следовательно, равна Сi.

Определение 5. Множество элементов алгебры, перестановочных со всеми элементами алгебры, называется центром алгебры.

Определение 6. Подмножество В алгебры называется подалгеброй алгебры А, если оно является подпространством векторного пространства А, и из того, что b1, b2ÎB, следует, что .

Можно доказать, что элементы Ci образуют базис центра Z групповой алгебры PG:

Алгебру можно записать, задав таблицу умножения базисных элементов

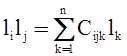. (20)

Элементы Cijk называются структурными константами алгебры. Для элементов Сi, образующих базис центра групповой алгебры, формула (20) принимает вид

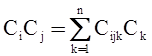. (21)

Теперь, на основании выражения (21), фиксируя индекс i (что обозначим, взяв этот индекс в скобки), получим матрицу C(i) коэффициентов Cijk. Эту матрицу можно рассматривать как матрицу линейного оператора , действующего в векторном пространстве, которым является центр алгебры Z. Действие его на базисные элементы Cj состоит в умножении Ci на Cj. Для того, чтобы записать матрицу C(i), надо рассмотреть столбец, в котором записаны произведения Ci на Cj. В результате получим матричное представление центра групповой алгебры. Матричное представление центра будет центром матричного представления всей алгебры. Иначе говоря, все матрицы C(i) коммутируют со всеми элементами матричного представления алгебры и между собой.

Мы приходим к задаче, аналогичной известной квантово-механической задаче: дана система коммутирующих между собой операторов, найти собственные значения и собственные векторы этих операторов. Оказывается, решение такой задачи имеет важное значение и для нахождения характеров неприводимых представлений.

Полученные выше матрицы Ci являются образующими элементами алгебры матриц, изоморфной алгебре Бозуа–Меснера, которая определяется следующим образом.

Назовем i-ой матрицей смежности Ai матрицу порядка, равного порядку группы G, строки и столбцы которой занумерованы элементами группы G, причем элементы матрицы Ai с номером (g, h), g, hÎG определяются как

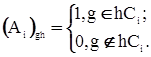
Матрицы Ai состоят из нулей и единиц, поэтому их называют (0, 1) – матрицами.

Определение 7. Алгеброй Боуза – Меснера называется подалгебра алгебры матриц Mn(C), порожденная (0, 1) – матрицами Ai, i=1, 2, …, d, удовлетворяющими следующим условиям:

1) A1=E, где Е – единичная матрица;

2) A1+A2+…+Ad=J, где J – матрица, все элементы которой равны единице;

3) , i¢Î[1, 2, …, d], где - матрица, транспонированная с матрицей Ai;

4) ;

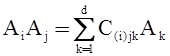5) .

Если построить матрицы смежности для группы G по указанному выше правилу, то они образуют базис алгебры Боуза–Меснера в соответствии с определением 7.

Если А – алгебра Боуза–Меснера, то из коэффициентов в соотношении 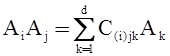можно образовать матрицы порядка d. Рассмотрим алгебру В, порожденную матрицами C1, C2, …, Cd, являющуюся подалгеброй алгебры d´d матриц Md(C). Эта алгебра изоморфна алгебре А Боуза–Меснера. В силу того, что в алгебре изоморфные объекты не различаются, будем называть ее также алгеброй Боуза–Меснера.