и

Сепарабельность отношений

Нечеткое отношение XRY называется сепарабeльным, если оно равно пересечению цилиндрических продолжений своих проекций, т.е. если R = Ç , т.е. mR (x,y) = (x)Ç (y).

Замечание. Если определено декартово произведение нечетких множеств (выше оно введено), то, очевидно, нечеткое отношение XRY сепарабельно, если оно является декартовым произведением своих проекций, т.е. R = R1'´R2'.

Пример (продолжение):

т.е. исходное отношение R несепарабельно.

Композиция двух нечетких отношений

Композиция двух нечетких отношений

Пусть R1 - нечеткое отношение R1: (X´ Y)®[0,1] между X и Y, и R2 - нечеткое отношение R2: (Y´Z)® [0,1] между Y и Z. Нечеткое отношение между X и Z, обозначаемое R2·R1, определенное через R1 и R2 выражением

mR1·R2 (x,z) = [mR1 (x,y)LmR1(y,z)],

называется (max-min)-композицией отношений R1 и R2.

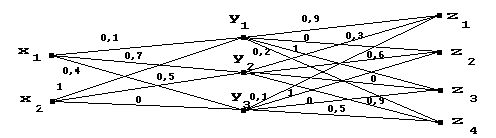
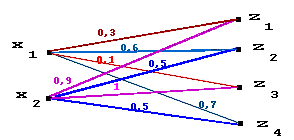
Примеры:

mR1·R2(x1, z1) = [mR1(x1, y1) L mR2 (y1, z1)] V [mR1(x1, y2) L mR2(y2, z1)] V [mR1(x1, y3) L mR2(y3, z1)] =

= (0,1L0,9)V(0,7L0,3)V(0,4L0,1) = 0,1V0,3V0,1 = 0,3

mR1·R2(x1,z2) = (0,1L0)V(0,7L0,6)V(0,4L 1) = 0V0,6V0,4 = 0,6

mR1·R2(x1,z3) = 0,1

.

.

mR1·R2(x2,z5) = 0,5

Замечание. В данном примере вначале использован "аналитический" способ композиции отношений R1 и R2 , т.е. i-я строка R1 "умножается" на j-й столбец R2 с использованием операции L, полученный результат "свертывается" с использованием операции V в m (xi,zj).

Ниже приведены графы, соответствующие R1 и R2, "склеенные" по Y. В полученном графе рассматриваем пути от xi к zj и каждому ставим в соответствие минимальный из "весов" его составляющих. Затем определяем максимум по всем путям из xi в zj, который и дает искомое m(xi,zj).

Свойства max-min композиции

Операция (max-min)-композиции ассоциативна, т.е.

R3·(R2·R1) = (R3·R2 )·R1,

дистрибутивна относительно объединения, но недистрибутивна относительно пересечения:

R3·(R2È R1) = (R3·R2)È (R3·R1),

R3·(R2Ç R1)¹(R3· R2)Ç(R3· R1).

Кроме того, для (max-min)-композиции выполняется следующее важное свойство: если R1ÌR2 то, R·R1 ÌR·R2.

(max-*) - композиция

В выражении mR1·R2(x, z) = [mR1(x, y)LmR2(y, z)] для (max-min)-композиции отношений R1 и R2 операцию L можно заменить любой другой, для которой выполняются те же ограничения, что и для L: ассоциативность и монотонность (в смысле неубывания) по каждому аргументу. Тогда:

mR1·R2(x, z) = [mR1(x, y)*mR1(y, z)]