2. Найдем точки пересечения с осями координат:

3. Т.к. все точки входят в область значений функции, то точек разрыва НЕТ.

4. Вертикальных асимптот у графика функции нет, т.к. нет точек разрыва. Правая и левая наклонные асимптоты имеют уравнение: , где:

т.к. правая и левая наклонные асимптоты совпадают, то уравнение имеет вид: , т.е. - уравнение горизонтальной асимптоты.

5. Найдем точки экстремума заданной функции. Для этого найдем ее первую производную:

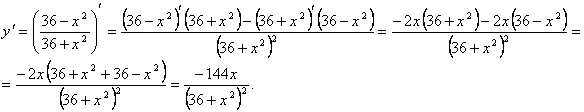
Т.к. если у функции есть точка экстремума, то в этой точке первая производная функции равна нулю, т.е. :

, дробь равна нулю, если ее числитель равен нулю, т.е. , отсюда , следовательно , значит точка - точка экстремума функции.

На участке производная > 0, значит, при , заданная функция возрастает.

На участке производная < 0, значит, при , заданная функция убывает (рис 2.).

Следовательно - точка максимума заданной функции .

6. Найдем участки выпуклости/вогнутости заданной функции. Для этого найдем ее вторую производную:

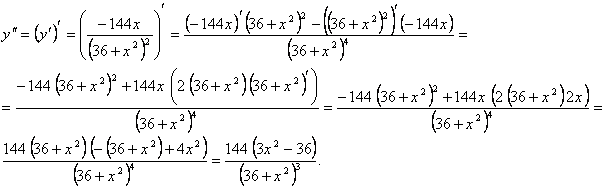
Т.к. если у функции есть точка перегиба, то в этой точке вторая производная функции равна нулю, т.е. :

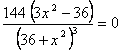, дробь равна нулю, если ее числитель равен нулю, т.е. , значит , тогда , отсюда

Отсюда , .

На участке производная 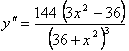>0, значит это участок вогнутости графика функции.

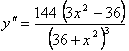На участке производная >0,

значит это тоже участок вогнутости графика функции.

Следовательно, при график заданной функции является вогнутым.

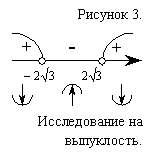
На участке производная 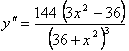<0, значит, при график заданной функции является выпуклым (рис. 3).

Следовательно, точки , - точки перегиба графика заданной функции .

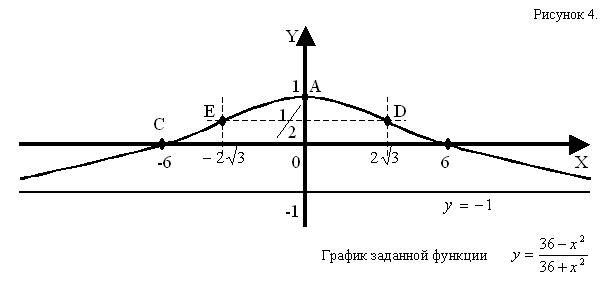Выполненные исследования заданной функции позволяют построить ее график (см. рис. 4).

Часть II.

Задание №8. Вопрос №8.

Фирма производит товар двух видов в количествах и. Задана функция полных издержек . Цены этих товаров на рынке равны и . Определить, при каких объемах выпуска достигается максимальная прибыль, найти эту прибыль.

, ,

Решение:

Пусть - функция прибыли, тогда

Найдем первые частные производные функции :