Метод функций Ляпунова переносится и на случай разрывной правой части системы

. (1)

Как было показано в первой главе, уравнения (1) сводятся к диф. включениям

(2)

Для диф. включений имеются два типа устойчивости: устойчивость и слабая устойчивость.

Определение 1.

Решение дифференциального включения (2) называется устойчивым (соответственно слабо устойчивым), если для каждого существует такое , что для каждого такого , что , каждое решение (соответственно некоторое решение) с начальным условием при существует и удовлетворяет неравенству

().

Асимптотическая устойчивость и слабая асимптотическая устойчивость определяются аналогично, но с дополнительным условием

Пример 1.

(). Решение асимптотически устойчиво. При любое другое решение достигает положения равновесия x=0 за конечное время, а при за бесконечное время.

Пример 2.

, F(x) – отрезок с концами kx и mx. - решение. Для других решений имеем

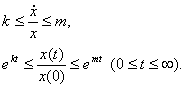
При асимптотически устойчиво,

при устойчиво,

при слабо асимптотически устойчиво,

при неустойчиво.

Для диф. уравнений с непрерывной правой частью известны теоремы Ляпунова об устойчивости и об асимптотической устойчивости [4]. В работе [17] сформулированы подобные теоремы для разрывных систем (1). Но для таких уравнений функция Ляпунова V(t,x) может не принадлежать .

Для функции (т.е. имеются непрерывные производныепервого порядка) определяются верхняя и нижняя производные в силу диф. включения (2):

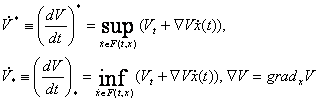
При почти всех t производная существует и удовлетворяет включению (2). При этих t существует

(3)

Теорема 1.

Пусть в замкнутой области D () для всех - непустое, ограниченное, замкнутое, выпуклое множество и функция -непрерывна по t, x; и существуют функции , для которых.

Тогда:

1) Если в D, то решение включения (2) устойчиво.

2) Если, кроме того, существуют функции причем , , (),, то решение асимптотически устойчиво.

Известные доказательства этих утверждений для диф. уравнений [4] остаются справедливыми и для диф. включений; при этом для оценки сверху функции V(t, x(t)) используют соотношение (3).

Теорема 2.

Если выполнены условия теоремы 1, но с заменой , то решение слабо устойчиво в случае 1) и слабо асимптотически устойчиво в случае 2).

Доказательство теоремы 2 приведено в [17].

Рассмотрим теперь случай, когда функция Ляпунова , но удовлетворяет условию Липшица в окрестности каждой точки области D. Тогда для любой абсолютно непрерывной функции x(t), значит и для любого решения, сложная функция V(t, x(t)) абсолютно непрерывна и почти всюду имеет производную по t. Однако решение может в течение некоторого промежутка времени идти по линии или поверхности, на которой grad V не существует, и производную dV/dt, нельзя, как в случае , представить в виде

Для :

. (4)

В случае функции V(t, x), удовлетворяющей условию Липшица, верхнюю и нижнюю производные от функции V в силу включения (2) можно определить как sup и inf правой части (4) по всем . Тогда теоремы 1и 2 сохраняются.

Пример 3.

Если , то нельзя пренебрегать отысканием dV/dt на линиях поверхностях разрыва функции f(t, x) даже в случае доопределения А.

Но этого недостаточно для применения теоремы 1, т.к. производные разрывны на осях координат, т.е. там же, где разрывны правые части системы. На оси Ox при доопределении А: