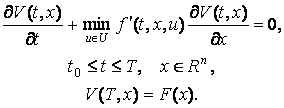(3.8)

Решив задачу (3.8) и определив функцию V(t,х), мож­но затем найти синтез оптимального управления u(t,x) из соотношения

. (3.9)

Возможность определять именно синтез оптималь­ного управления является характерной чертой ме­тода динамического программирования, особенно существенной в задачах управления при неполной информации. Использование метода динамическо­го программирования при решении конкретных за­дач сопряжено с необходимостью решать нелиней­ное уравнение в частных производных (3.8), а также с необходимостью дополнительного исследования оптимальности управления, полученного из (3.9).

2.3. Линейно-квадратичная задача

Выше была описана универсальная техника ре­шения задач оптимального управления, основанная на применении принципа максимума или метода динамического программирования. Наряду с этими методами при исследовании специальных классов задач оптимального управления могут быть исполь­зованы специальные приемы, эффективные имен­но для данного класса задач. Преимущество этих специальных приемов состоит в том, что с их помо­щью иногда можно проще осуществить аналогич­ное исследование рассматриваемой конкретной за­дачи.

Один из таких подходов, опирающийся на тео­рию двойственности выпуклых функций, эф­фективен для задач, линейных по фазовым коорди­натам. При этом вычисление минимума критерия качества в исходной задаче сводится к вычислению максимума некоторого вспомогательного функцио­нала. Это, в частности, дает возможность изучать задачи, в которых оптимального управления не су­ществует. Другой подход, эффективный для линей­ных задач (то есть задач линейных и по фазовым координатам, и по управлениям), основан на ис­пользовании классической проблемы моментов.

Отмеченные выше трудности использования об­щих необходимых условий оптимальности также приводят к необходимости выделения конкретных классов задач, для которых оказывается возмож­ным эффективное построение решения. Линейная квадратичная задача представляет собой один из та­ких классов. Проиллюстрируем применение к ней принципа максимума и метода динамического про­граммирования на следующем скалярном примере:

(3.10)

(3.11)

Здесь a, b, g, h, T - заданные постоянные, причем , h > 0, начальное положение системы х0 также задано, ограничения на управление отсутствуют. Требуется определить оптимальное управление сис­темой (3.10) и соответствующее этому оптимальному управлению минимальное значение критерия каче­ства (3.11). Применим вначале принцип максимума. Функция . Поэтому урав­нение (3.5) для сопряженной переменной имеет вид

. (3.12)

Условие максимума функции Н по u приводит к ра­венству . Следовательно, , то есть

(3.13)

Подставим выражение (3.13) для оптимального уп­равления в уравнение (3.10). В результате получим краевую задачу относительно переменных x и .

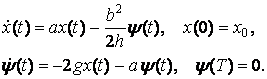(3.14)

Будем искать функцию в виде , где функция P(t) подлежит определению. С учетом (3.13) оптимальное управление тогда равняется

. (3.15)

Кроме того, подставляя выражение для в (3.14), получаем, что функция P(t) есть решение диффе­ренциального уравнения Рикатти

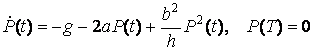(3.16)

Уравнение (3.16) интегрируется в явном виде мето­дом разделения переменных. После того как функ­ция Р(t) найдена, оптимальное управление дается выражением (3.15), причем дальнейшие вычисления констант показывают, что минимальное значение критерия качества

(3.17)

Исследуем теперь ту же задачу (3.10), (3.11), используя метод динамического программирования. Уравне­ния (3.8) с учетом (3.10), (3.11) принимают вид

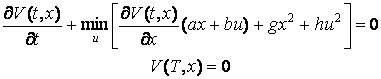(3.18)

Из (3.18) вытекает, что оптимальное управление дает­ся выражением

(3.19)

Соотношения (3.18), (3.19) означают, что функция V есть решение нелинейного уравнения в частных производных первого порядка

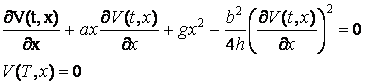(3.20)

Решение задачи (3.20) будем искать в виде . Подставляя это выражение в соотношения (3.20) и приравнивая к нулю коэффициенты при х2, заключаем, что функция P(t) удовлетворяет уравнению (3.16). Из уравнения (3.19) далее следует, что опти­мальное управление имеет вид (3.15), а минимальное значение критерия качества дается формулой (3.17). Таким образом, для линейно-квадратической зада­чи принцип максимума и метод динамического программирования позволяют построить опти­мальное управление (3.15) (причем в виде синтеза) и определить минимальное значение критерия каче­ства (3.17). Последнее зависит только от начального положения системы х0 и величины P(0), то есть мо­жет быть определено заранее, до фактической реа­лизации процесса управления. Аналогично и опти­мальное управление может быть найдено в зависимости только от времени t. Для этого надле­жит определить P(t) как решение задачи Коши (3.16), затем подставить управление (3.15) с найденным Р(t) в уравнение (3.10) и решить его, определив х(t), нако­нец, подставить x(t) в (3.15) и получить программное оптимальное управление.

2.4. Задача об успокоении твердого тела

Одним из хорошо изученных классов задач оп­тимального управления являются задачи линейного оптимального быстродействия, а также некото­рые задачи успокоения движения твердого тела (возникающие, например, в теории управления ле­тательными аппаратами). Рассмотрим в качестве примера одну из них, именно задачу об успокоении твердого тела, вращающегося относительно центра масс О. Обозначим: , i = 1, 2, 3, - главные цент­ральные оси инерции тела, xi - проекция вектора кинетического момента х на ось Охi, и А, В, С - глав­ные центральные моменты инерции твердого тела. Управление и движением твердого тела осуществля­ется парой поворотных двигателей, которые можно расположить под любым углом относительно тела. Движение тела относительно центра масс описыва­ется уравнениями Эйлера