По действующей программе эти задачи в курсе 8 класса (бывший 7 класс) заменены такой: В прямоугольном треугольнике даны: гипотенуза c и острый угол . Найдите катеты, их проекции на гипотенузу и высоту, опущенную на гипотенузу.

Вводятся основные тригонометрические тождества:

, , , .

В частности, основное тригонометрическое тождество выводится из формулировки теоремы Пифагора:

, .

Учащиеся знакомятся с некоторыми свойствами функций острого угла: 1) при возрастании острого угла и возрастают, а - убывает; 2) для любого острого угла : , ; которые формулируются как теоремы. Их доказательство связывается с соотношениями острых углов в прямоугольном треугольнике:

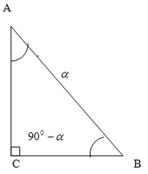
, , тогда , .

,

тогда из равенства правых частей получаем:

.

, тогда .

Вывод свойства возрастания и убывания выглядит так:

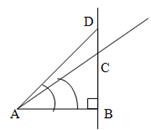
Пусть и - острые углы, и , и она пересекает стороны углови в точках и соответственно.

Так как , то точка лежит между точками и , тогда . А значит, по свойству наклонных, (через сравнение их проекций). Так как , , то косинус убывает. А так как , то синус возрастает.

2. Методика введения определений тригонометрических функций углов от до

Расширение области определения тригонометрических функций от до происходит в теме: "Декартовы координаты на плоскости".

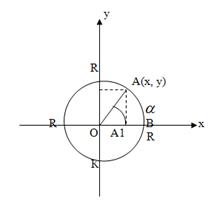
Рассмотрим окружность с центром в начале координат произвольного радиуса R. Откладываем в полуплоскость угол . Пусть точка имеет координаты и . , , то из треугольника : , .

Определяются значения и этими формулами для любого угла α (для 0-исключается).

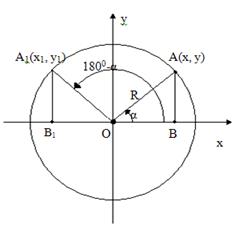
Можно найти значения этих функций для углов 900, 00, 1800. Доказывается, что для любого угла α , 00<α<1800, .

повернем подвижный радиус на угол 1800-α=

по гипотенузе и острому углу: => OB1=OB; A1B1=AB => x = -x1,y = y1=>

Итак, в школьном курсе геометрии понятие тригонометрической функции вводится геометрическими средствами ввиду их большей доступности.