Изучение тригонометрического материала в школьном курсе математики

Отрезок оси , с помощью которого находятся значения синуса, называется линией синусов.

Для построения графика синуса вне этого отрезка заметим, что . Поэтому во всех точках вида , где , значения синуса совпадают, и, следовательно, график синуса на всей прямой получается из построенного графика с помощью параллельных переносов его вдоль оси .

Для построения графика косинуса следует вспомнить, что . Следовательно, значение косинуса в произвольной точке равно значению синуса в точке . Это значит, что график косинуса получается из графика синуса с помощью параллельного переноса на расстояние в отрицательном направлении оси . Поэтому график функции также является синусоидой.

Для функций и определяется аналогично. Область определения - множество всех чисел, где .

Построение графика: проведем касательную к единичной окружности в точке .

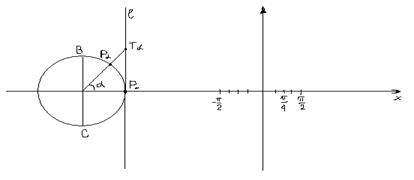
Пусть произвольное число, для которого . Тогда точка не лежит на оси ординат, и, следовательно, прямая пересекает в некоторой точке с абсциссой 1. Найдем ординату этой точки. Для этого заметим, что прямая проходит через точки и . Поэтому она имеет уравнение .

Абсцисса точки , лежащей на этой прямой, равна 1. Из уравнения прямой находим, что ордината точки равна . Итак, ордината точки пересечения прямых и равна . Поэтому прямую называют линией тангенсов.

Нетрудно доказать, что абсцисса точки пересечения прямой с касательной m к единичной окружности, проведённой через точку , равна при .

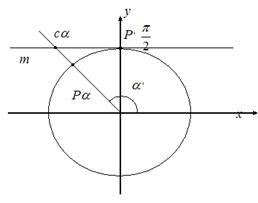
Поэтому прямую m называют линией котангенсов.

Область значений - вся числовая прямая. Докажем это для функции . Пусть - произвольное действительное число. Рассмотрим точку . Как только что было показано, равен . Следовательно, функция принимает любое действительное значение , ч.т.д.

Построение графика аналогично построению .

Можно построить схему, позволяющую изобразить график тригонометрических функций:

1) Начертить единичную окружность, горизонтальный диаметр которой служит продолжением оси . Разделить её на равные части (например,16).

2) Для функции выбираем отрезок , для функции - и делим их на то же равное число частей.

3) По окружности находим соответствующее число значений этих функций.

4) Точки пересечения горизонтальных линий, отвечающих значениям функций и вертикальных линий, отвечающих значениям аргумента, представляют собой точки графика.

4. Тождественные преобразования тригонометрических выражений. Тригонометрические уравнения и неравенства и методика обучения решению

Тригонометрический материал изучается в школьном курсе в несколько этапов.

1) Функции тригонометрических функций для углов от до

Страница:

Последние рефераты