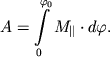Динамика твердого тела
или
|
|
(3.9) |
поскольку в случае твердого тела ![]()
Уравнение (3.9) и есть основное уравнение динамики вращательного движения твердого тела вокруг неподвижной оси. Его векторная. форма имеет вид:
|
|
(3.10) |
Вектор ![]() всегда направлен вдоль оси вращения, а
всегда направлен вдоль оси вращения, а ![]() - это составляющая вектора момента силы вдоль оси.
- это составляющая вектора момента силы вдоль оси.
В случае ![]() получаем
получаем ![]() соответственно и момент импульса относительно оси
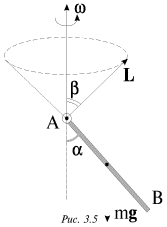
соответственно и момент импульса относительно оси ![]() сохраняется. При этом сам вектор L, определенный относительно какой-либо точки на оси вращения, может меняться. Пример такого движения показан на рис. 3.5.
сохраняется. При этом сам вектор L, определенный относительно какой-либо точки на оси вращения, может меняться. Пример такого движения показан на рис. 3.5.
|
|
|
Рис. 3.5. |
Стержень АВ, шарнирно закрепленный в точке А, вращается по инерции вокруг вертикальной оси таким образом, что угол ![]() между осью и стержнем остается постоянным. Вектор момента импульса L, относительно точки А движется по конический поверхности с углом полураствора
между осью и стержнем остается постоянным. Вектор момента импульса L, относительно точки А движется по конический поверхности с углом полураствора ![]() однако проекция L на вертикальную ось остается постоянной, поскольку момент силы тяжести относительно этой оси равен нулю.
однако проекция L на вертикальную ось остается постоянной, поскольку момент силы тяжести относительно этой оси равен нулю.
Кинетическая энергия вращающегося тела и работа внешних сил (ось вращения неподвижна).
Скорость i -й частицы тела
|
|
(3.11) |
где ![]() - расстояние частицы до оси вращение Кинетическая энергия
- расстояние частицы до оси вращение Кинетическая энергия
|
|
(3.12) |
так как угловая скорость вращения для всех точек одинакова.
В соответствии с законом изменения механической энергии системы элементарная работа всех внешних сил равна приращению кинетической энергии тела:
|
|
(3.13) |
Работа внешних сил при повороте тела на конечный угол ![]() равна
равна
|
|
(3.14) |
опустим, что диск точила вращается по инерции с угловое скоростью ![]() и мы останавливаем его, прижимая какой-либо предмет к краю диска с постоянным усилием. При этом на диск будет действовать постоянная по величине сила
и мы останавливаем его, прижимая какой-либо предмет к краю диска с постоянным усилием. При этом на диск будет действовать постоянная по величине сила ![]() направленная перпендикулярно его оси. Работа этой силы
направленная перпендикулярно его оси. Работа этой силы
|
|
где ![]() - радиус диска,
- радиус диска, ![]() - угол его поворота. Число оборотов, которое сделает диск до полной остановки,
- угол его поворота. Число оборотов, которое сделает диск до полной остановки,
|
|
где ![]() - момент инерции диска точила вместе с якорем электромотора.
- момент инерции диска точила вместе с якорем электромотора.
Замечание. Если силы таковы, что ![]() то работу они не производят.
то работу они не производят.
Свободные оси. Устойчивость свободного вращения.
При вращении тела вокруг неподвижной оси эта ось удерживается в неизменном положении подшипниками. При вращении несбалансированных частей механизмов оси (валы) испытывают определенную динамическую нагрузку, Возникают вибрации, тряска, и механизмы могут разрушиться.