А2 - случайная величина Х приняла значение x2,

………………………………………………………

Аn - случайная величина Х приняла значение An.

Очевидно, что сумма событий A1 A2, . , An является достоверным событием, так как хотя бы одно из значений x1, x2, xn случайная величина обязательно принимает.

Поэтому P (A1 È А2 È . È Аn) = 1.

Кроме того, события А1, А2, ., An - несовместны, т. к. случайная величина при однократном осуществлении опыта может принять только одно из значений х1, х2, ., xn. По теореме сложения для несовместных событий получаем

Р(А1)+Р(А2)+ .+Р(Аn)=1,

т. е. p1+p2+ . +pn = 1, или, короче,

Следовательно, сумма всех чисел, расположенных во второй стро­ке Таблицы 1, дающей закон распределения случайной величины X, должна быть равна единице.

ПРИМЕР 1. Пусть случайная величина Х - число очков, выпавших при подбрасывании игральной кости. Найти закон распределения (в виде таблицы).

Случайная величина Х принимает значения

x1=1, х2=2, … , x6=6

с вероятностями

р1= р2 = … = р6 =

Закон распределения задается таблицей:

Таблица 2

ПРИМЕР 2. Биноминальное распределение. Рассмотрим случайную величину Х — число появлений события А в серии из независимых опытов, в каждом из которых А насту­пает с вероятностью р.

Случайная величина Х может, очевидно, принимать одно из следующих значений:

0, 1, 2, ., k, ., n.

Вероятность события, состоящего в том, что случайная величина Х примет значение, равное k, определяется формулой Бернулли:

Рn(k)= где q=1- р.

Такое распределение случайной величины называется биномиальным распределением или распределением Бернулли. Распределение Бернулли полностью задается двумя параметрами: числом n всех опытов и вероятностью р, с которой событие происходит в каждом отдельном опыте.

Условие для биномиального распределения принимает вид:

Для доказательства справедливости этого равенства достаточно в тождестве

(q+рх)n=

положить x=1.

ПРИМЕР 3. Распределение Пуассона. Так называется распределение вероятностей вида:

Р(k)=.

Оно определяется одним единственным (положительным) параметром а. Если ξ – случайная величина, имеющая распределение Пуассона, то соответствующий параметр а - есть среднее значение этой случайной величины:

а=Мξ=, где М – математическое ожидание.

Случайная величина равна:

ПРИМЕР 4. Показательное распределение.

Если время является случайной величиной, обозначим его τ, таково, что

где 0<λ=const, t ³ 0, причем, если t=0, то P(t)=0.

Среднее значение случайной величины t есть:

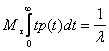
Плотность распределения имеет вид:

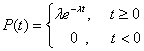
4) Нормальное распределение

Пусть - независимые, одинаково распределенные случайные величины и пусть Если слагаемые достаточно малы, а число n достаточно велико, - если при n à ∞ математическое ожидание случайной величины Мξ и дисперсия Dξ равная Dξ=M(ξ–Мξ)2, таковы, что Мξ~а, Dξ~σ2, то

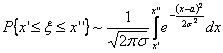- нормальное или гауссово распределение

Функция распределения имеет вид:

.

5) Геометрическое распределение. Обозначим ξ число испытаний, предшествующих наступлению первого "успеха". Если считать, что каждое испытание длится единицу времени, то можно считать ξ временем ожидания до первого "успеха". Распределение имеет вид:

Р(k)=p(1-p)k, (k=0, 1, 2) p>0

6) Гипергеометрическое распределение.

Имеется N – объектов среди которых n - "особых объектов". Среди всех объектов случайным образом выбирается k-объектов. Найти вероятность того, что среди отобранных объектов находится равно r - "особых объектов". Распределение имеет вид:

Р(x=r)=

7) Распределение Паскаля.

Пусть x - общее число "неудач", предшествующих поступлению r-го "успеха". Распределение имеет вид:

Функция распределения имеет вид:

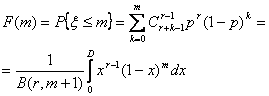
Равновероятностное распределение подразумевает, что случайная величина x может принимать любые значения на отрезке [a,b] с одинаковой вероятностью. Плотность распределения при этом вычисляется как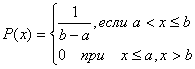

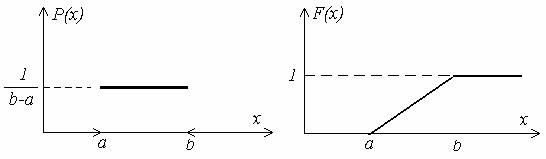
Графики плотности распределения и функция распределения представлены ниже.

Перед тем, как объяснить понятие «белый шум», необходимо дать ряд определений.

Случайной функцией называют функцию неслучайного аргумента t, которая при каждом фиксированном значении аргумента, является случайной величиной. Например, если U – случайная величина, то функция X(t)=t2U – случайная.

Сечением случайной функции называют случайную величину, соответствующую фиксированному значению аргумента случайной функции. Таким образом, случайную функцию можно рассматривать как совокупность случайных величин {X(t)}, зависящих от параметра t.