Функция linterp(vx, vy, xd) – возвращает оценку значения в точке x, вычисленную методом линейной интерполяции на основе значений из векторов x и y;

· vx – вещественный вектор, элементы которого должны идти в порядке возрастания и соответствовать значениям х;

· vy – вещественный вектор одного размера с vх. Его элементы соответствуют значениям y;

· xd – значение переменной x, в которой нужно проинтерполировать величину y. Предполагается, что х лежит в интервале изменения элементов vx.

Задаем значения х и у в виде матриц:

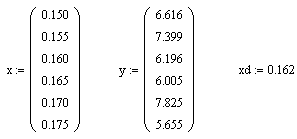
Находим функцию f(x):

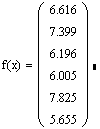
Строим график функции:

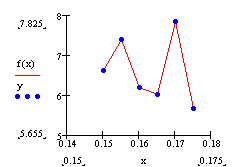
рис. 4.1

График проходит через узлы интерполяции, значит функция задана верно.

4.2. Решение с помощью параболического сплайна

Сплайн – это математическая модель гибкого, тонкого стержня из упругого материала. Стержень закрепляется в двух соседних узлах с заданными углами наклона. Стержень длиннее, чем расстояние между двумя точками. Линия, которую описывает сплайн-функция, напоминает по форме гибкую линейку, закреплённую в узловых точках (откуда и название: spline – гибкая линейка).

Функция cspline(vx, vy) – возвращает вектор коэффициентов кубического сплайна vs, который используется функцией interp для построения кубического сплайна, интерполирующего данные, представленные в векторах vx и vy. На поведение сплайна на концах условий не налагается. Вектор vs становится первым параметром функции interp.

Функция interp(vs, vx, vy, x) – возвращает интерполированное значение в точке х, полученное с помощью кубических сплайнов на основе данных, представленных в векторах vx и vy.

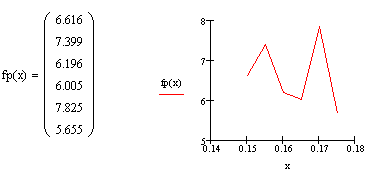
рис. 4.2

4.3. Решение с помощью линейной аппроксимации

Найдем коэффициенты аппроксимирующего полинома с помощью функций interceptи slope.

Функция intercept(vx, vy) –свободный член уравнения регрессии. Равен отрезку, отсекаемому линией регрессии на оси ординат, и определяется по формуле:

Функция slope(vx, vy) – коэффициент линейного уравнения регрессии. Определяет тангенс угла наклона линии регрессии к оси х, используя формулу:

Применим эти функции для получения свободного члена и коэффициента регрессии

Записываем аппроксимирующий полином и получаем приближенное значение функции в заданной точке.

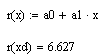
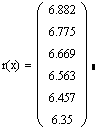
Построим график аппроксимирующего полинома и таблично заданной функции.

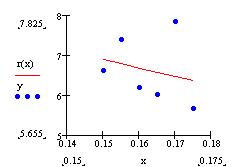
рис. 4.3

4.4. Решение с помощью метода наименьших квадратов

Суть метода: сумма квадрата разности между аппроксимирующей функцией и функцией заданной таблично должна быть минимальной.

Задаем степень аппроксимирующего полинома.

при m=2

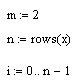
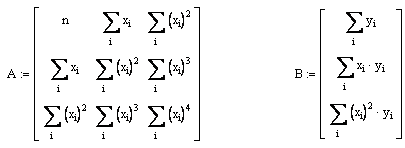
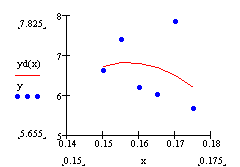
рис. 4.4

при m=3

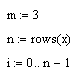
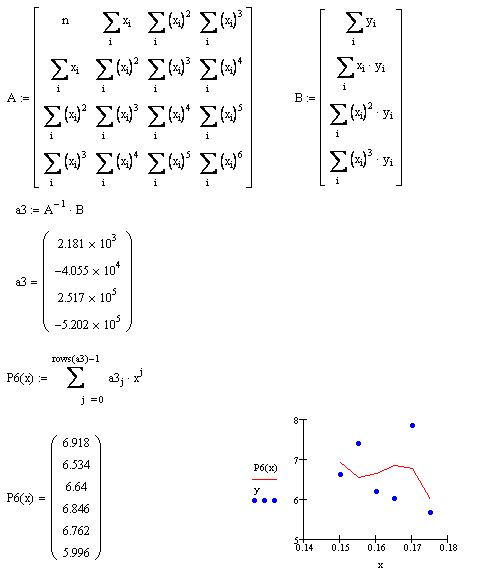
рис. 4.5

4.5. Решение с помощью полиноминальной регрессии

Задача регрессии заключается в получении параметра приближённой функции таким, чтобы функция отличалась от таблично заданной функции с наименьшей среднеквадратичной погрешностью.

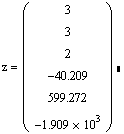
при m=2

Функция regress(vx, vy, m) – вектор, требующий interp для нахождения полинома порядка m, наилучшим образом приближающего данные из vx и vy.

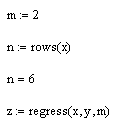
submatrix(A, ir, jr, ic, jc,) – субматрица, состоящая из элементов матрицы А, содержащихся в строках от ir по jr и столбцах с ic по jc.

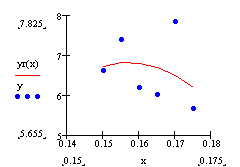
рис. 4.6

при m=3

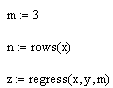
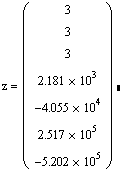
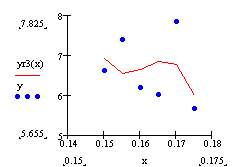
рис. 4.7

4.6. Графики таблично заданной функции в одних осях координат

Для сравнения всех функций и полученных вычислений построим общий график:

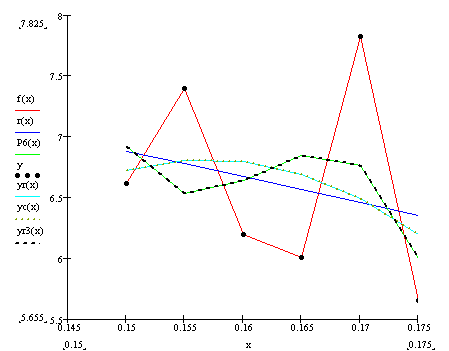
рис. 4.8

7. Анализ полученных результатов

Проведя исследование функции различными методами, мы получили примерно одинаковые результаты, так как при исследовании разными методами таблично заданная функция ведет себе по разному. Но, исследуя функцию с помощью метода наименьших квадратов и полиномиальной регрессии при одинаковых значениях порядка полинома графики функций совпадают, что говорит о правильности всех вычислений. Так же на это указывает тот факт, что среднеквадратичное отклонение получилось меньше единицы.

Задание 5. Решение дифференциальных уравнений

1. Решить дифференциальное уравнение методом Рунге-Кутта.

При решении дифференциального уравнения искомой величиной является функция. Для обыкновенных дифференциальных уравнений неизвестная функция – функция одной переменной. Дифференциальные уравнения в частных производных – это дифференциальные уравнения, в которых неизвестной является функция двух или большего числа переменных. MathCAD имеет ряд встроенных функций, предназначенных для решения дифференциального уравнения. Каждая из этих функций предназначена для численного решения обыкновенного дифференциального уравнения. В результате решения получается матрица, содержащая значения функции, вычисленные на некотором множестве точек (на некоторой сетке значений). Для каждого алгоритма, который используется при решении дифференциальных уравнений, MathCAD имеет различные встроенные функции. При решении поставленной задачи будем использовать метод Рунге-Кутта, применяя функцию rkfixed(y, x1, x2, n, F)