Содержание

Содержание

Модель парной линейной регрессии

Оценивание параметров функции парной линейной регрессии

Связь оценок параметров функции парной линейной регрессии с выборочными числовыми характеристиками

Коэффициент детерминации

Литература

Модель парной линейной регрессии

Предположим, что у нас есть все основания считать, что два экономических показателя взаимосвязаны. Например, уровень инфляции и уровень безработицы в какой-либо стране или спрос на товар и цена товара, темп роста валового внутреннего продукта (ВВП) и доходность ценной бумаги.

В нашем распоряжении имеется набор данных, полученных в результате статистических наблюдений за интересующими нас показателями. Такие данные приводятся в различных периодических изданиях, журналах, газетах и бюллетенях и относятся ко всем сферам экономики.

Используя указанные эмпирические данные, мы хотим подобрать (если это возможно!) функцию, которая связывает эти экономические показатели. Безусловно, эта задача повлечет за собой целый ряд других задач (насколько хорошо мы подобрали функцию, значима или нет зависимость между показателями и т.д.), но пока рассмотрим подход к её решению.

Договоримся в дальнейшем зависимую (эндогенную) переменную обозначать через у, и называть результирующим признаком, а независимую (экзогенную) переменную через x и называть фактором. Тогда упорядоченный набор значений переменных (x; y) это двумерная выборка. Очень часто в литературе переменную х называют объясняющей переменной.

Пример 1. В качестве примера такой выборки рассмотрим следующую выборку значений темпа роста ВВП (переменная x) и доходности акций компании Widget (переменная y) [13]:

(5,7; 14,3), (6,4; 19,2), (7,9;23,4), (7;15,6), (5,1;9,2), (2,9; 13).

Эти же данные можно было бы записать в виде следующей таблицы:

Таблица 1.

Или изобразить в виде точек на плоскости в ДСК

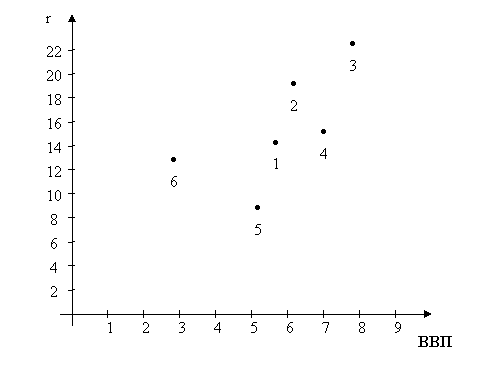
Рис.1 Корреляционное поле.

Характер расположения точек на рисунке, называемом корреляционным полем, подсказывает, что зависимость между переменными x и y в среднем близка к линейной, то есть

.

Или

(1)

Однако если зависимость между переменными была бы линейной, то все точки лежали бы на одной прямой, значит нужно внести коррективу. Включим в модель, которую мы пытаемся подобрать, ещё одну переменную, которую назовем ошибкой наблюдения (или неучтенными в модели факторами) и обозначим через e.

Уравнение (1) перепишем в виде

(2)

Относительно переменных e i сделаем следующие допущения. Будем считать, что:

1. Ошибки наблюдения ei являются случайными величинами, распределенными по нормальному закону.

2. Математическое ожидание всех случайных величин ei равно нулю:

3. Все ошибки наблюдения ei имеют одинаковую (но неизвестную!) дисперсию:

4. Случайные величины ei и ej, i¹j, предполагаются независимыми друг от друга.

Замечание 1. Известно, что выражение для момента корреляции двух случайных величин можно записать в виде:

.

Так как величины ei и ej по четвертому предположению независимы, то они и некоррелированные, то есть . В силу второго предположения Поэтому получаем, что

.▲

Замечание 2. Относительно факторной переменной х будем рассматривать два предположения:

● переменная х носит детерминированный (неслучайный) характер;

● переменная х является случайной величиной.

Каждый раз будет оговорено, в рамках какого из двух предположений рассматривается изучаемая модель. ▲

Определение 1. Условия 1-4 называются условиями Гаусса – Маркова.

Замечание 3. Вернемся к условиям Гаусса – Маркова и прокомментируем их. Предположение о том, что означает, что ошибки наблюдения поступают с разными знаками и компенсируют друг друга. То есть исключается ситуация, когда ошибки систематически появляются с одним и тем же знаком. Поэтому в случае, когда , говорят, что систематическая ошибка равна нулю.

Требование постоянства дисперсии случайных величин ei говорит о том, что все наблюдения производятся с равной точностью. Поэтому в русскоязычной литературе говорят, что имеет место равноточная схема наблюдений. В англоязычной литературе предположение о том, что имеет место равенство, называют условием гомоскедастичности (homoscedasticity). Если то говорят, что имеет место гетероскедастичность ошибок.

Условие независимости случайных величин ei и ej, i¹j, которое автоматически влечет за собой их некоррелированность, означает, что ошибка i-ого наблюдения не влияет на результат j-го.▲

Замечание 4. Вернемся к уравнению (2). В этом уравнении коэффициенты b0 и b1 являются неизвестными параметрами, которые подлежат нахождению.

В силу того, что переменные ei в уравнении (2) являются случайными величинами, то и уi , которые связаны с ними функционально, будут носить случайный характер. Вычислим математическое ожидание и дисперсию уi, предполагая, что переменная х носит детерминированный характер: