;

Так как случайные величины ei распределены по нормальному закону, то по теореме о том, что линейное преобразование случайных величин, распределенных по нормальному закону, сохраняет закон распределения (изменяются только параметры распределения), можем сделать вывод: случайные величины уi распределены по нормальному закону распределения с математическим ожиданием и одинаковыми дисперсиями s2.▲

Таким образом, математическое ожидание случайной величины уi будет зависеть от такого, какое значение примет переменная хi, (которая в общем случае также является случайной величиной), то есть будет являться условным математическим ожиданием.

Функция переменной х, задающая значение условного математического ожидания, называется функцией регрессии первого рода или модельной функцией регрессии. Так как в нашем распоряжении только информация эмпирического характера, то мы будем работать с функцией регрессии второго рода или, так называемой эмпирической функцией регрессии, служащей статистической оценкой модельной функцией регрессии.

Будем обозначать эмпирическую функцию регрессию . Таким образом,

, (3)

(4)

Эта функция показывает, как «в среднем» изменяются значения случайной величины у, в зависимости от того, какие значения примет х. График функции регрессии одной переменной называют линией регрессии.

Определение 2. Функция (3), задающая среднее значение переменной у, при условии, что независимая переменная х приняла фиксированное значение, называется функцией регрессии.

Вернемся к уравнениям (1) и (2) и перепишем их с учетом (3), (4), получим:

, (5)

(6)

Определение 3. Если выполняются условия Гаусса-Маркова и имеет место уравнение (5) (или (6)), то говорят, что задана классическая нормальная регрессионная модель.

Подводя итог, отметим, что когда мы говорим о регрессионной модели, то мы имеем в виду уравнение (5), когда речь идет о функции регрессии, то рассматривается уравнение (3). Регрессионная модель включает в себя функцию регрессии и неучтенные в модели факторы, носящие по предположению случайных характер.

Оценивание параметров функции парной линейной регрессии

В эконометрике приходится сталкиваться с двумя ситуациями. Уже имеющаяся математическая модель, построенная, исходя из тех или иных экономических предпосылок, проверяется эконометрическими методами на ее соответствие новым экономическим условиям. Иными словами, известная экономическая модель проверяется на «правильность». Еще одна ситуация, с которой приходится встречаться, заключается в том, что необходимо построить саму модель, то есть, подобрать функцию, которая аппроксимирует зависимость между теми или иными показателями. Такая попытка построения модели была предпринята нами в примере 1. Однако, даже после того, как сам вид модели задан, остается важная задача отыскания неизвестных параметров модели, или, выражаясь более корректно, оценивания параметров регрессионной модели. Существуют различные подходы и методы к решению задачи оценивания параметров. В этом параграфе рассмотрим метод поиска оценок неизвестных коэффициентов, называемый методом наименьших квадратов (МНК или OLS- ordinary least squares).

Разберем сначала идею самого метода. Изобразим на корреляционном поле фактические значения уi, гипотетическую линию регрессии , (которая исходя из нашего предположения является прямой линией и которая нам на самом деле неизвестна) и ошибки ei. (Рис.2)

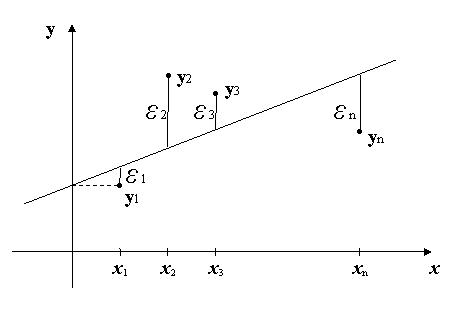
Рис.2. График функции линейной регрессии.

Неизвестные коэффициенты b0 и b1 будем подбирать так, чтобы сумма квадратов отклонений ei (фактических значений уi от линии регрессии ) была наименьшей. Таким образом, неизвестные коэффициенты b0 и b1 будем искать исходя из условия минимума функции двух переменных

равной:

= .

Или

=.

Следовательно, МНК дает возможность отыскать неизвестные коэффициенты b0 и b1 исходя из условия минимума суммы квадратов ошибок, обусловленных влиянием неучтенных в регрессионной модели факторов.

Перепишем выражение для минимизируемой функции, используя уравнение (2) в следующем виде:

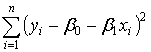= . (1)

Запишем необходимое условие экстремума этой функции двух переменных:

,

.

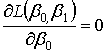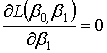Или:

,

.

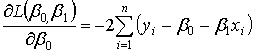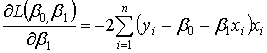Приравняв обе частные производные к нулю:

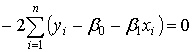, (2)

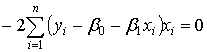, (3)

и, выполнив алгебраические преобразования, получим следующую систему:

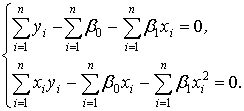
Неизвестные коэффициенты не зависят от индекса суммирования, поэтому, вынося их за знак суммы, перепишем последнюю систему в окончательном виде: