доверительный интервал для β

доверительный интервал для α

Мы не можем на данном уровне значимости принять гипотезу β=0 или α =0, т.к. обе не попадают в доверительный интервал. Т.е. оба коэффициента значимы.

Прогноз

Точечный прогноз для x =8, т.е. подсчитаем уровень рентабельности при темпе роста заработной платы в 8%.

Интервальный прогноз

Построенная регрессия хорошо объясняет зависимость и годится для прогнозирования.

Пример 2

Прибыль предприятия зависит от себестоимости реализованной продукции и управленческих расходов за период. Данные представлены в таблице 2. Построим зависимость прибыли от этих факторов.

Для регрессии вида

Найдем коэффициенты

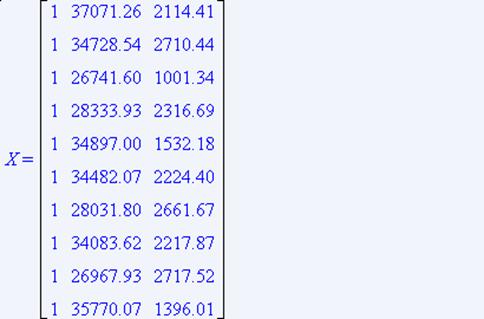
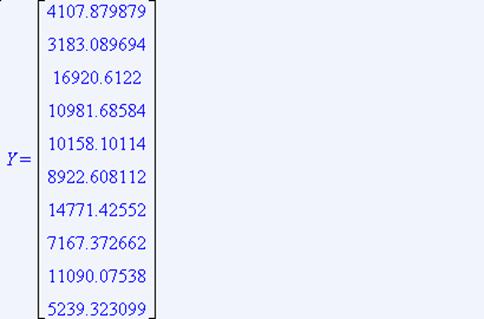
Найдем обратную матрицу

Дополнительные миноры

Их определители

Союзная матрица

Союзная транспонированная матрица

Делим каждый элемент на определитель, получаем

β=

Уравнение регрессии имеет вид

Нарисуем график

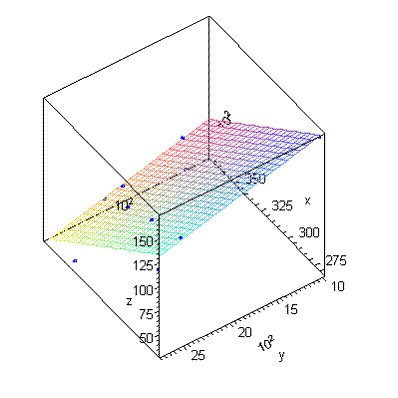
Найдем множественный коэффициент детерминации

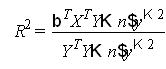
Показывает, что 81,17% вариации Y обусловлено вариацией X1 и X2.

Проведем F-тест.

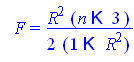
Регрессия значима и годится для прогнозирования.

Пример 3

Рентабельность производственной деятельности характеризует окупаемость издержек, связанных с производством и реализацией продукции, эффективность предпринимательской деятельности. Увеличение показателей рентабельности в динамике свидетельствует о повышении эффективности деятельности, степени доходности, прибыльности организации.

Рассмотрим вопрос динамики рентабельности производственной деятельности в динамике. Произведем линейное сглаживание. Исходные данные представлены в таблице 3 приложения.

Для регрессии вида

найдем коэффициенты

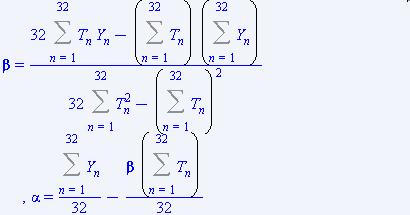
Вычислим

Откуда

Тогда линейная регрессия будет иметь вид

Нарисуем точки и регрессию:

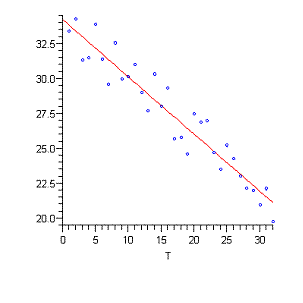
Найдем остатки