a. На множестве вещественных чисел определена операция сложения, удовлетворяющая следующим аксиомам:

a.1.

a.2.

a.3.

a.4.

a.5.

b. Введем операцию умножения:

b.1.

b.2.

b.3.

b.4.

b.5.

c. Дистрибутивность. Распределительный закон.

c.1.

Множество, элементы которого удовлетворяют a, b, c – числовое поле.

Примеры: множество вещественных и рациональных чисел.

Отношение порядка.

На множестве вещественных чисел вводится отношение порядка , т.е. , которое удовлетворяет следующим аксиомам:

1. выполняется

2.

3.

4.

5.

6.

Из этих аксиом следует, что для любого а и b , выполняются три случая:

1. a <b

2. (a =b)

3. b<a

Множество, на котором вводится отношение порядка, удовлетворяющее аксиомам 1-6, называется линейной упорядоченностью. И множество вещественных чисел, и множество рациональных чисел – линейно упорядоченное поле

Аксиома непрерывности вещественных чисел

Пусть , причем и : , тогда

Множеством вещественных чисел называется линейно упорядоченное непрерывное числовое поле.

Замечание: Аксиома непрерывности гарантирует, что каждому вещественному числу соответствует единственный тип числовой прямой и, наоборот, каждой числовой прямой соответствует единственное вещественное число.

Представление (модель) вещественного числа.

Можно доказать, что аксиомам удовлетворяют десятичные дроби, причем конечные (периодические) соответствуют рациональным числам, а бесконечные (непериодические) – иррациональным числам.

Т.к. бесконечные дроби нельзя использовать при вычислениях (не представимы в ЭВМ), то в реальных расчетах пользуются исключительно рациональными числами, но доказано, что любое вещественное число можно с любой степенью точности представить рациональным числом.

Свойство числового множества (следует из свойства упорядоченности).

Множество - ограничено сверху, если .

Число M – верхняя граница множества X.

Любое число - точка верхней границы, т.к.

Итак, верхних границ бесконечно много.

Наименьшая из всех верхних границ – верхняя грань множества Х (sup X – супремум икс)

Множество - ограничено снизу, если .

Число В – верхняя граница множества X.

Любое число - точка нижней границы, т.к.

Наибольшая из всех нижних границ – нижняя грань множества Х (inf X).

Множество называется ограниченным, если оно ограничено и снизу и сверху.

Теорема: Любое непустое, ограниченное сверху (снизу) множество, имеет верхнюю (нижнюю) грань.

Понятие абсолютной величины вещественного числа.

На упорядоченном числовом множестве введем понятие модуля (абсолютной величины) вещественного числа:

Свойства:

1.

2.

3.

4.

5.

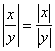
6.

7.

Решение простейших неравенств с модулем.

Эквивалентность неравенств:

1.

2.

геометрический смысл:

1.

2.