4. Если ф-ия имеет в т. а, конечный предел, неравный нулю то найдется такая в т. а, в которой - ограниченная.

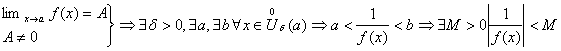
5. Если f(x), имеет в т. а отрицательный конечный предел, то найдется такое значение этой точки, в котором ф-ия отрицателная.

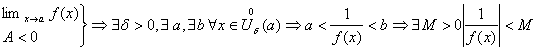
Бесконечно малые ф-ии и их свойства:

Опр:- бесконечно малая при , если

Свойства:

Пусть и являются бесконечно малыми при , а - ограничена, то бесконечно малыми является алгебраическая сумма ф-ий f(x) и j(x), произведения их и произведения ф-ий на ограниченную.

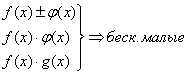
Представвление ф-ии, имеющей конечный предел.

Теорема: Для того чтобы ф-ия имела конечный предел А в точке х=а, небходимо и достаточно, чтобы =А+a(х), где a(х)- бесконечно малая при .

Доказательство:

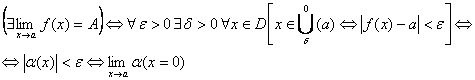
Алгебраические свойства фунцций имеющих конечный предел в точке а.

Пусть 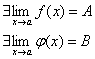, тогда:

1. Существует предел алгебраической суммы этих ф-ий,равный алгебраической сумме этих пределов.

2. Существует предел произведения ф-ий Þ произведение пределов

3. Если предел знаменателя неравен 0 и B неравно 0 то

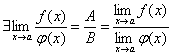
Следствие.

Из 1 и 2 следует, что константы можно выносить за знак предела

Бесконечно большие и их свойства

Опр. Ф-ия называется бесконечно большой в точке а, если ее предел в этой точке равен бесконечности.

Свойства

Пусть и - бесконечно большие ф-ии в точке а.

Ф-ия j(х) имеет предел в точке а, отличный от 0

Ф-ия a(х) и b(ч) – бесконечно малые

Тогда справедливы следующие утверждения:

1. Произведение двух бесконечно больших ф-ий – бесконечно большая ф-ия.

2. Произведение бесконечно больших на ф-ию, имеющую отличный от нуля предел - бесконечно большая.

3. Ф-ия, обратная величине бесконечно большой – есть бесконечно малая, и наоборот.

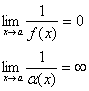
Доказательство 2):

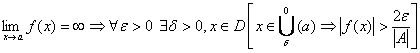
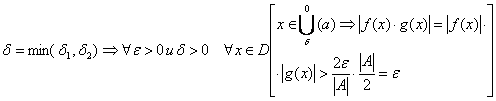
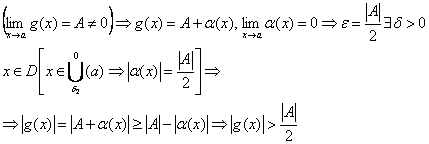
Доказательство 3):

Односторонние пределы в конечной точке и их связь с пределом в этой точке.

В определении предела окрестности точки а – симметричный интервал с центром в этой точке, т.е. требуется существование значений ф-ий как справа от точки а , так и слева от нее.

Когда а – граничная точка D(f)- такая ситуация невозможна. В этом, случае вводится понятие одностороннего предела, в определении которого фигурирует левые и правые полуокрестности точки а

- левосторонний предел, если в левой d полуокружности точки А, значения ф-ии лежат в e-окрестности точки А

Аналогично дается определение правостороннего предела.

Теорема: Для того, чтобы в точке а существовал предел ф-ии, необходимо и достаточно существования и равенства левостороннего и правостороннего пределов

Доказательство:

1. Необходимость:

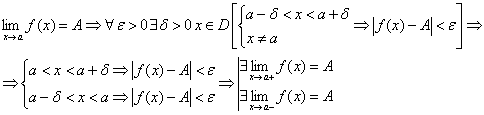
2. Достаточность:

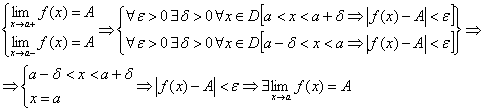
Числовые последовательности

Задача, по которой каждому N числу, ставится в соответствие единственное вещественное число – называется числовой последовательностью.

Числовая последовательность – ф-ия натурального аргумента.

Обозначается:

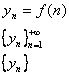
Последовательность, множество значений которой состоит из одного числа – стационарная.

Так как числовая последовательность – не симметричное множество, то для него не существует понятия четности, нечетности, периодичности. Зато сохраняются свойства, связанные с упорядоченностью.

Свойства:

1) Ограниченность.

a) последовательность ограничена сверху, если

b) последовательность ограничена снизу, если

c) последовательность ограничена, если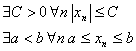

2) Монотонность.