1) вычисляя сразу всю площадь, 2) вычисляя по частям.

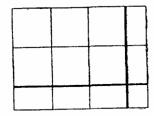
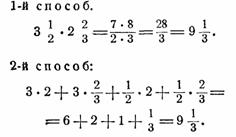Рис.14

Учащиеся получают наглядное представление о втором способе умножения.

Полезно показать, что при вычислении вторым способом приме­няется распределительный закон умножения.

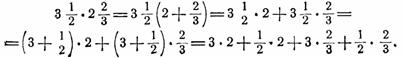
Следует подчеркнуть учащимся, что совпадение произведений, полученных 1-м и 2-м способами, показывает на справедливость распределительного закона и в том случае, когда оба сомножи­теля — смешанные числа.

Изучая умножение дробей, следует обратить внимание учащихся еще на одну особенность умножения на дробь, отличающую его от умножения на целое число.

При умножении на правильную дробь полученное произведение меньше множимого (или от умножения на правильную дробь данное число уменьшается). Следует требовать обоснование этого вывода рассуждением и иллюстрировать примерами.

Рассмотрим систему примеров на умножение на неправильную дробь.

Вывод. При умножении на неправильную дробь, не равную еди­нице, произведение получается больше множимого.

После этого следует предложить учащимся сделать общий вы­вод относительно того, в каком случае произведение получается больше множимого, в каком случае меньше множимого, в каком случае оно равно множимому. Следует задавать учащимся следую­щие контрольные вопросы. Например: на какое число нужно умно­жить число 5, чтобы произведение получилось больше 5? равно 5? меньше 5? Приведите примеры.

Деление на дробь

Делению на дробь предпосылается и в программе и в стабиль­ном учебнике нахождение числа по данной величине его дроби. Рас­суждения ведутся по такой схеме.

Пример. Найти число которого равны 20.

Обозначим неизвестное число буквой х, тогда условие задачи запишется:

от х равны 20.

Так как часть числа находится умножением, то вместо от х можно написать х· или, пользуясь переместительным законом, · х. Следовательно, можно написать: от х равны 20, или х· = 20, или ·х = 20, так как в случае бук­венного сомножителя принято знак умножения пропускать. Решение. 1) = 20 : 5 = 4; 2) х = 4 · 6 = 24.

Как и при нахождении дроби числа, при нахождении числа по данной величине его дроби необходимо рассмотреть различные случаи.

Определение деления числа на дробь остается то же, что и при делении целых чисел. Эту мысль необходимо подчеркнуть учащимся. Для того чтобы соблюдалась одна и та же система изучения обрат­ных действий, следует начать с повторения образования действия деления для целых чисел, затем перейти к рассмотрению примера на умножение на дробь и образовать две обратные задачи.

Например: 27 · = 12.

Составим обратную задачу, взяв за искомое число множитель. Эта задача решается делением целого числа на целое, которое рас­смотрено раньше.

Составим вторую обратную задачу, взяв за искомое множимое.

Запишем:

х·=12.

Эта задача и для дробных чисел решается действием деления 12 : = х.

Так как х·= 12 или ·х = 12, то, чтобы найти х, мы находим число которого равны 12, отсюда х = (12 : 4) · 9 = 27.

При помощи такого рода рассуждений, основой которых служит определение, учащиеся приходят к выводу, что при делении на дробь отыскивается число по данной величине его дроби. Рассмотрев примеры на умножение целого числа на дробь в случае дробного произведения и дроби на дробь и составив обратные задачи, уча­щиеся получают все случаи деления дробей. Проделав несколько упражнений, учащиеся выводят .правило деления целого на дробь, также дроби на дробь.

Неправильно строить изучение деления на дробь, взяв за опре­деление, что разделить какое-нибудь число на дробь - значит найти число по данной величине его дроби. Это противоречит научному построению изучения действий над числами, при котором вычитание я деление любых чисел определяются как действия, обратные сложению и умножению.

Полезно напомнить учащимся, что так как умножение обладает переместительным законом, то для отвлеченных чисел деление на дробь имеет одинаковый смысл независимо от того, какой из двух Сомножителей - множимое или множитель - является данным и какой искомым.

Но при решении конкретных задач деление на дробь в том случае, когда искомым является множитель (деление по содержанию), имеет другой смысл по сравнению с тем случаем, когда искомым является множимое. Например, рассмотрим задачу.

Из 6м проволоки нужно сделать прутики для счетов, длиною каждый по м. Сколько выйдет таких прутиков?

Для решения этой задачи 6м : м, в этом случае частное показывает, сколько раз м содержится в 6 м. или во сколько раз 6м больше м.

Для отыскания частного можно провести следующие рассуждения: 6м = м, м содержится в м 8 раз.

Но можно рассуждать и так: 6м: м = х; м · х = 6 м. Но, по переместительному закону умножения, · х = х·.

Следовательно, и в этом случае мы можем деление выполнять по тому же правилу, что и при нахождении всего числа по данной его части.

Рассмотрим вторую задачу.

Площадь одного участка га, другого га. Какую часть пло­щадь второго участка составляет от площади первого?