Оглавление

Введение

§1. Предварительные сведения о бинарных квадратичных

формах

§2. О периодах неопределенных бинарных квадратных

форм

§3. Об оценке сверху числа приведенных неопределимых

бинарных квадратичных форм

§4. О диагональных формах и оценке снизу числа

классов в ряде

Литература

Введение

Арифметическая теория квадратичных форм берет свое начало с утверждения Ферма о представимости простых чисел суммой двух квадратов.

Теория квадратичных форм впервые была развита французским математиком Лагранжем, которому принадлежат многие идеи в этой теории, в частности, он ввел важное понятие приведенной формы, с помощью которого им была доказана конечность числа классов бинарных квадратичных форм заданного дискриминанта. Затем эта теория была значительно расширенна Гауссом, который ввел много новых понятий, на основе которых ему удалось получить доказательства трудных и глубоких теорем теории чисел, ускользавших от его предшественников в этой области.

Перейдем теперь к краткой характеристике содержания нашей работы, посвященной некоторым вопросам теории неопределенных бинарных квадратичных форм.

Вначале нашей работы приводятся предварительные общие сведения о бинарных квадратичных формах. Во втором параграфе, посвященном периодам неопределенных квадратичных форм поставлены и решены два вопроса о двусторонних формах (теоремы 1,2). В третьем параграфе дается элементарное доказательство известной оценки для числа приведенных неопределенных бинарных квадратичных форм заданного дискриминанта. Наконец, в последнем параграфе устанавливаем, что диагональные формы одного и того же положительного дискриминанта не эквивалентны (теорема 3) и применяем этот результат к оценке снизу для числа классов в каждом роде неопределенных квадратичных форм (теорема 4).

§1. Предварительные сведения о бинарных квадратичных форм.

В данном параграфе мы дадим те общие понятия и свойства, касающиеся бинарных квадратичных форм, на которые будем опираться в дальнейшем изложении.

Определение 1. Бинарной квадратичной формой называется однородный многочлен второй степени от двух переменных, т.е. выражение вида

(1)

где - вещественные числа.

Коэффициенты - называются соответственно первым, вторым и третьим коэффициентами (1) и для краткости такую форму будем обозначать, следуя Гауссу [2], через так, что

В алгебраической теории квадратичных форм (т.е. в теории квадратичных форм над полями) рассматриваются формы, у которых второй коэффициент без множителя , т.е.

.

Но в арифметической теории квадратичных форм (т.е. в теории форм над кольцами и в первую очередь над кольцом целых чисел) более предпочтительной является запись вида (1).

Определение 2. Бинарная квадратичная форма (1) называется классически целой (или целочисленной по Гауссу), если в ней коэффициенты являются целыми числами.

Мы будем в основном рассматривать только классические квадратичные формы и называть их просто численными.

Определение 3. Бинарные целочисленные квадратичные формы и называются собственно эквивалентными, если существует линейная подстановка переменных

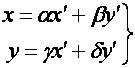(2)

с целыми коэффициентами и определителем , переводящая форму в форму , т.е. такая, что выполняется равенство

(3)

и несобственно эквивалентными, если целочисленная подстановка (2) с определителем переводит форму в форму . Эквивалентность таких форм обозначаем так: ~

Из (3) и (2) следуют соотношения

(4)

связывающие коэффициенты двух эквивалентных форм и .

Определение 4. Дискриминантом бинарной квадратичной формы называется число .

Предложение 1. Эквивалентные бинарные квадратичные формы имеют один и тот же дискриминант.

Доказательство. Пусть форма эквивалентна (собственно или несобственно) форме. Тогда по определению 3 существуют целые числа с определителем , при которых выполнены соотношения (4). Из них получаем

,

т.е. предложение 1 доказано.

Заметим, что обратное утверждение вообще говоря неверно, т.е. из того, что бинарные квадратичные формы имеют один и тот же дискриминант еще не следует, что они эквивалентны. Следующий общий факт приведем без доказательства.

Предложение 2. Отношение собственной эквивалентности бинарных квадратичных форм обладает свойствами рефлексивности, симметричности и транзитивности.

Определение 5. Если для квадратичной формы и для целого числа при некоторых целых и выполняется равенство , то говорят, что квадратичная форма представляет число .