Subroutine Горизонт (X1, Y1, X2, Y2; Верх, Низ)

Эта программа использует линейную интерполяцию для заполнения массивов горизонтов между X1 и X2

Max (a, b) – определяет большее из a и b

Min (a, b) – определяет меньшее из a и b

проверка вертикальности наклона

if (X2 - X1) = 0 then

Верх (X2) = Max (Верх (X2), Y2)

Низ (X2) = Min (Низ (X2), Y2)

else

Наклон = (Y2 - Y1)/(X2 - X1)

for x = X1 to X2 step 1

y = Наклон * (x - X1) + Y1

Верх (x) = Max (Верх (x), y)

Низ (x) = Min (Низ (x), y)

next x

end if

return

подпрограмма вычисления пересечения текущей кривой с горизонтом

Subroutine Пересечение (X1, Y1, X2, Y2, Массив; Xi, Yi)

Эта процедура вычисляет пересечение двух отрезков прямых

Массив содержит информацию о соответствующем горизонте

Sign – функция принимающая значения -1, 0, 1, если знак её аргумента <0, =0, >0 соответственно

проверка бесконечности наклона

if (X2 – X1) = 0 then

Xi = X2

Yi = Массив (X2)

else

вычисление пересечения

обход начинается с самой левой используемой точки

пересечение считается обнаруженным, когда изменяется знак разности значений y

Наклон = (Y2 – Y1)/(X2 – X1)

Ysign = Sign (Y1 + Наклон - Массив (X1 + 1))

Csign = Ysign

Yi = Y1 + Наклон

Xi = X1 + 1

while Csign = Ysign

Yi = Y1 + Наклон

Xi = X1 + 1

Csign = Sign (Yi - Массив (Xi))

end while

выбирается ближайшее целое число

if |Yi - Наклон - Массив (X1 – 1)| £ |Yi - Наклон - Массив (X1)| then

Yi = Y1 – Наклон

Xi = X1 – 1

end if

end if

return

В приведенных выше алгоритме и примере функция у = f (x, z) рассматривалась только при z = const. Часто бывает удобно вычерчивать кривые, полагая постоянными как z, так и x. При этом возникает эффект перекрестной штриховки. На первый взгляд мо­жет показаться, что перекрестную штриховку можно получить пу­тем наложения двух результатов, образованных плоскостями z = const и x = const. Однако это не так. Верный результат получается при обработке тех кривых из числа лежащих в плоскостях z = const и x = const, которые ближе всего к горизонтальным при обычном порядке их следования. Однако после обработки каж­дой кривой, самой близкой к горизонтальной, необходимо обраба­тывать участки кривых, лежащих в ортогональных ей плоскостях, которые находятся между указанной кривой и кривой, следующей за ней. Разумеется, при обработке обеих последовательностей кри­вых нужно использовать одни и те же массивы верхнего и нижнего плавающих горизонтов. Если используется перекрестная штриховка, то не надо формировать левое и правое боковые ребра.

3.2. Алгоритм Робертса

Алгоритм Робертса представляет собой первое известное решение задачи об удалении невидимых линий . Это математически элегантный метод, работающий в объектном пространстве. Алгоритм, прежде всего, удаляет из каждого тела те ребра или грани, ко­торые экранируются самим телом. Затем каждое из видимых ребер каждого тела сравнивается с каждым из оставшихся тел для опре­деления того, какая его часть или части, если таковые есть, экрани­руются этими телами. Поэтому вычислительная трудоемкость ал­горитма Робертса растет теоретически как квадрат числа объек­тов. Именно этот факт привёл к снижению инте­реса к алгоритму Робертса. Однако математические методы, ис­пользуемые в этом алгоритме, просты, мощны и точны. Кроме то­го, этот алгоритм можно использовать для иллюстрации некоторых важных концепций. Наконец, более поздние реализации алго­ритма, использующие предварительную приоритетную сортировку вдоль оси z и простые габаритные или минимаксные тесты, демонстрируют почти линейную зависимость от числа объектов.

В алгоритме Робертса требуется, чтобы все изображаемые тела или объекты были выпуклыми. Невыпуклые тела должны быть разбиты на выпуклые части. В этом алгоритме вы­пуклое многогранное тело с плоскими гранями должно представ­ляться набором пересекающихся плоскостей. Уравнение произвольной плоскости в трехмерном пространстве имеет вид

ах + by + cz+ d = 0 (3.1)

В матричной форме это выглядит так:

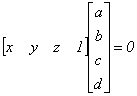
или

где представляет собой плоскость. Поэтому любое выпуклое твердое тело можно выразить матрицей тела, состоящей из коэффициентов уравнений плоскостей, т. е.

где каждый столбец содержит коэффициенты одной плоскости.

Напомним, что любая точка пространства представима в однородных координатах вектором

Более того, если точка [S] лежит на плоскости, то [S]*[P]T = 0. Если же [S] не лежит на плоскости, то знак этого скалярного произведения показывает, по какую сторону от плоскости расположена точка. В алгоритме Робертса предпола­гается, что точки, лежащие внутри тела, дают положительное ска­лярное произведение.

Хотя уравнение плоскости (3.1) содержит четыре неизвестных коэффициента, его можно нормировать так, чтобы d = 1 следовательно, трех неколлинеарных точек достаточно для определения этих коэффициентов. Подстановка координат трех неколлинеарных точек (x1, y1, z1), (x2, y2, z2), (x2, y2, z2) в нормированное уравнение (3.1) дает:

ax1 + by1 + cz1 = -1

ax2 + by2 + cz2 = -1

ax3 + by3 + cz3 = -1

В матричной форме это выглядит так:

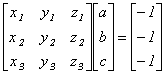
или

(3.2)

Решение этого уравнения дает значения коэффициентов уравнения плоскости:

Другой способ используется, если известен вектор нормали к плоскости, т. е.

n = ai + bj + ck

где i, j, k - единичные векторы осей x, y, z соответственно. Тогда уравнение плоскости примет вид

ax + by + cz + d = 0 (3.3)

­

Величина d вычисляется с помощью произвольной точки на плоско­сти. В частности, если компоненты этой точки на плоскости (х1, y1, z1) то:

d = - (aх1 + by1 + cz1) (3.4)

Поскольку объем вычислений в алгоритмах удаления невидимых линий или поверхностей растет с увеличением числа многоугольни­ков, для описания поверхностей выгодно использовать многоуголь­ники с более чем тремя сторонами. Эти многоугольники могут быть как невыпуклыми, так и неплоскими. Метод, предложенный Мартином Ньюэлом, позволяет найти как точное решение для уравнений плоскостей, содержащих плоские многоугольники, так и «наилучшее» приближение для неплоских многоугольников. Этот метод эквивалентен определению нормали в каждой вершине мно­гоугольника посредством векторного произведения прилежащих ре­бер и усреднения результатов. Если a, b, c, d – коэффициенты уравнения плоскости, то