Если Di > 0, то диагональная точка ( xi + 1, уi – 1 ) находится вне окружности, т. е. это случаи З и 4 на рис.2.6. В данной ситуа­ции ясно, что должен быть выбран либо пиксел ( xi + 1, уi – 1 ), т. е. mD, либо ( xi, уi – 1 ), т. е. mV. Аналогично разбору предыдущего случая критерий выбора можно получить, рассматривая сна­чала случай З и проверяя разность между квадратами расстояний от окружности до диагонального mD и вертикального mV пикселов, т. е.

При d\ < 0 расстояние от окружности до вертикального пиксе­ла ( xi, уi – 1 ) больше и следует выбрать диагональный шаг mD, к пикселу ( xi + 1, уi – 1 ). Напротив, в случае d\ > 0 расстояние от окружности до диагонального пиксела больше и следует выбрать вертикальное движение к пикселу ( xi, уi – 1 ). Таким образом,

при d £ 0 выбираем mD в ( xi + 1, уi – 1 )

при d < 0 выбираем mV в ( xi, уi – 1 )

Здесь в случае d = 0, т. е. когда расстояния равны, выбран диагональный шаг.

Проверка компонент d\ показывает, что

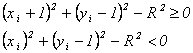
поскольку для случая З диагональный пиксел ( xi + 1, уi – 1 ) находится вне окружности, тогда как вертикальный пиксел ( xi, уi – 1 ) лежит внутри ее. Это позволяет записать d\ в виде

Дополнение до полного квадрата члена ( xi )2 с помощью добавления и вычитания 2xi + 1 дает

Использование определения Di приводит выражение к виду

Теперь, рассматривая случай 4, снова заметим, что следует выбрать вертикальный пиксел ( xi, уi – 1 ), так как y является монотонно убывающей функцией при возрастании x. проверка компонент d\ для случая 4 показывает, что

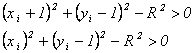
поскольку оба пиксела находятся вне окружности. Следовательно, d\ > 0 и при использовании критерия, разработанного для случая 3, происходит верный выбор mV.

Осталось проверить только случай 5 на рис.2.7, который встречается, когда диагональный пиксел ( xi + 1, уi – 1 ) лежит на окружности, т. е. Di = 0. Проверка компонент d показывает, что

Следовательно, d > 0 и выбирается диагональный пиксел ( xi + 1, уi – 1 ). Аналогичным образом оцениваем компоненты d\:

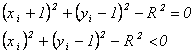
и d < 0, что является условием выбора правильного диагонально­го шага к ( хi + 1, уi – 1 ). Таким образом, случай Di = 0 подчиня­ется тому же критерию, что и случай Di < 0 или Di > 0.

Подведем итог полученных результатов:

Di < 0

d £ 0 выбираем пиксел ( хi + 1, уi ) ® mH

d > 0 выбираем пиксел ( хi + 1, уi – 1 ) ® mD

Di > 0

d\ £ 0 выбираем пиксел ( хi + 1, уi – 1 ) ® mD

d\ > 0 выбираем пиксел ( хi , уi – 1 ) ® mV

Di = 0 выбираем пиксел ( хi + 1, уi – 1 ) ® mD

Легко разработать простые рекуррентные соотношения дня реализации пошагового алгоритма. Сначала рассмотрим горизонталь­ный шаг mH к пикселу ( хi + 1, уi ). Обозначим это новое положение пиксела как ( i + 1 ). Тогда координаты нового пиксела и значение Di равны

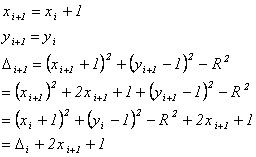
Аналогично координаты нового пиксела и значения Di для шага mD к пикселу ( хi + 1, уi – 1 ) таковы:

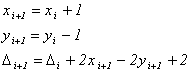
То же самое для шага mV к ( хi, уi – 1 )

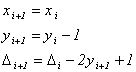
Реализация алгоритма Брезенхема для окружности приводиться ниже.

Пошаговый алгоритм Брезенхема для генерации окружности в первом квадранте

все переменные целые

xi = 0

yi = R

Di = 2(1 – R)

Предел = 0

1 Plot ( xi, yi )

if yi £ Предел then 4

выделение случая 1 или 2, 4 или 5, или 3

if Di < 0 then 2

if Di > 0 then 3

if Di = 0 then 20

определение случая 1 или 2

2 d = 2Di + 2yi – 1

if d £ 0 then 10

if d > 0 then 20

определение случая 4 или 5

3 d = 2Di + 2xi – 1

if d £ 0 then 20

if d > 0 then 30

выполнение шагов

шаг mH

10 xi = xi +1

Di = Di +2xi + 1

goto 1

шаг mD

20 xi = xi +1

yi = yi – 1

Di = Di +2xi – 2yi + 2

goto 1

шаг mV

30 yi = yi – 1

Di = Di – 2xi + 1

goto 1

4 finish

2.5. Растровая развёртка сплошных областей

До сих пор речь шла о представлении на растровом графическом устройстве отрезков прямых линий. Однако одной из уникальных характеристик такого устройства является возможность представ­ления сплошных областей. Генерацию сплошных областей из простых описаний ребер или вершин будем называть растровой раз­верткой сплошных областей, заполнением многоугольников или за­полнением контуров. Для этого можно использовать несколько методов, которые обычно делятся на две широкие категории: растровая развертка и затравочное заполнение.

В методах растровой развертки пытаются определить в порядке

сканирования строк, лежит ли точка внутри многоугольника или контура. Эти алгоритмы обычно иду от «верха» многоугольника или контура к «низу».

В методах затравочного заполнения предполагается, что извест­на некоторая точка (затравка) внутри замкнутого контура. В алго­ритмах ищут точки, соседние с затравочной и расположенные внут­ри контура. Если соседняя точка расположена не внутри, значит, обнаружена граница контура. Если же точка оказалась внутри контура, то она становится новой затравочной точкой и поиск продолжается рекурсивно.

2.6. Растровая развёртка многоугольников

Можно разработать эффективный метод растровой развёртки многоугольников, если воспользоваться тем фактом, что соседние пикселы, вероятно, имеют одинаковые характеристики (кроме пикселов граничных рёбер). Это свойство называется пространственной когерентностью.

Характеристики пикселов на данной строке изменяются только там, где ребро многоугольника пересекает строку. Эти пересечения делят сканирующую строку на области.

Для простого многоугольника на рис. 2.7 строка 2 пересекает многоугольник при x = 1 и x = 8.

Получаем три области:

x < 1 вне многоугольника

1 £ x £ 8 внутри многоугольника

x > 8 вне многоугольника

Строка 4 делится на пять областей:

x < 1 вне многоугольника

1 £ x £ 4 внутри многоугольника