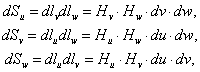
и элемента объема

- Напишите общие выражения градиента, дивергенции, ротора, лапласиана в криволинейных координатах.

- Выражение градиента скалярной функции в криволинейных координатах

Как видим, градиент в криволинейных координатах зависит не только от значения функции в точке, но и от значения масштабных коэффициентов данной системы координат и направления единичных орт осей.

Принцип определения дивергенции вектора через его проекции, примененный в случае прямоугольных координат, сохраним и теперь, т.е.

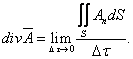
Выражение лапласиана в криволинейных координатах:

Ротор будем искать обычным образом:

Теперь запишем выражение вектора :

Выражение удобно записать через определитель

- Чему равны коэффициенты Ламе в цилиндрических и сферических координатах?

- Определим значения коэффициентов Ламе цилиндрических координат. Для этого запишем выражения для элементов длин координатных линий

С другой стороны, известно, что

Сопоставляя попарно эти равенства, приходим к выводу, что

- Связь сферических координат с прямоугольными определяется соотношениями

Элементы длин координатных линий найдем, сопоставляя попарно выражения из двух систем

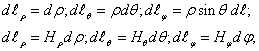
Из этого имеем:

- Запишите выражения градиента, дивергенции, ротора, лапласиана в цилиндрических и сферических координатах.

2. ТЕОРИЯ ГЕОФИЗИЧЕСКИХ ПОЛЕЙ

2.1. Формулы Грина. Задачи Дирихле и Неймана. Использование формул Грина, фундаментальная формула Грина. Гармонические функции, их свойства. Краевые задачи Дирихле и Неймана. Функция Грина. Решение задачи Дирихле для сферы.

- Объясните назначение фундаментальной формулы Грина.

Данная формула носит название фундаментальной формулы Грина. Она позволяет вычислять значение функции , непрерывной вместе со своими производными, внутри области , если известны ее значения и значения на поверхности , а также значения во всех внутренних точках области. Использовать формулу на практике крайне сложно, т. к. требуются весьма подробные сведения об определяемой функции.

- Дайте определение гармонической функции.

- Функция называется гармонической, если она непрерывна вместе со своими производными первого и второго порядков внутри конечной области и в каждой точке области удовлетворяет уравнению Лапласа

- Сформулируйте теорему о среднем значении гармонической функции.

- Теорема о среднем (теорема Гаусса). Значение гармонической функции во всякой внутренней точке равно интегральному среднему ее значений, взятых по поверхности любой сферы радиуса с центром в т., лежащей целиком внутри области , т.е.

- Напишите общий вид функции Грина. Поясните, в чем состоит сложность ее определения.

Нахождение функции Грина в конкретных случаях представляет весьма сложную задачу, т.к. она зависит не только от формы поверхности, но и от положения полюса внутри нее.

- Напишите формулу, по которой решается внутренняя краевая задача Дирихле.

,

Это выражение дает решение уравнения Лапласа внутренней задачи Дирихле. Для этого решения должны быть заданы значения функции на поверхности и значения на ней нормальной производной функции Грина.

Даже в таком упрощенном виде формула сложна для применения, т. к. для каждой поверхности и для каждого положения точки необходимо находить аналитическое выражение функции Грина. Задача решена лишь для некоторых поверхностей.

2.2. Гравитационное и магнитное поля. Потенциал притяжения, три его вида. Свойства потенциала объемных масс и его производных. Потенциал магнитного диполя, намагниченного тела конечных размеров, однородно намагниченного шара. Формула Пуассона.

- Напишите, чему равен потенциал притяжения точечной массы.

Эта функция носит название потенциала притяжения точечной массы.

Если массы распределены в объеме непрерывно и имеют объемную плотность , то тело можно разбить на элементы , массы которых равны . Каждый такой элемент можно заменить действием материальной точки, расположенной внутри элемента и имеющей массу .

- Поясните, как определяется потенциал объемных масс, простого и двойного слоя.

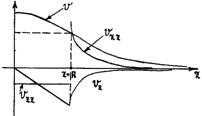
- Нарисуйте график изменения потенциала объемных масс.