Содержание.

Введение

1. Основы зонной теории твердых тел

2. Квантовая статистика

3. Квантовая теория теплоемкости

4. Проводимость металлов и полупроводников

5. Контактные и термоэлектрические явления

6. Диффузия и дрейф носителей заряда в полупроводниках

ВВЕДЕНИЕ.

В последние десятилетия внутри самой физики на первое место выдвинулась физика твердого тела (ФТТ) - наука о строении и свойствах твердых тел и происходящих в них явлениях. ФТТ составляет основную часть фундамента современной техники. Все конструкционные материалы - это материалы твердые: тысячи марок стали, разнообразные металлические сплавы, полимеры. Великое множество твердых материалов используется непосредственно - металлические проводники, полупроводниковые, лазерные и оптические кристаллы, изоляторы, магнитные сплавы, режущий инструмент и т.д. и т.п. Не существует ни одной области техники, где так или иначе не использовались бы твердые материалы с самыми разнообразными механическими, электрическими, оптическими, тепловыми, антикоррозионными и др. свойствами. Физика полупроводников оказала очень существенное влияние на современную технику и цивилизацию. Без квантовой теории твердого тела появление таких конкретных вещей, как полупроводниковые диоды, транзисторы, светодиоды, твердотельные лазеры, фотоэлементы, солнечные батареи, интегральные схемы и т. д. было бы не возможно.Потребность техники в новых материалах очень велика и их создание невозможно без знания ФТТ. По количеству научных публикаций и числу физиков, занимающихся ФТТ, эта область составляет примерно половину современной физики.

Задача этого курса - описать основы строения твердых тел с точки зрения квантовой механики и, опираясь на основные физические законы, объяснить протекающие в них процессы. Любое твердое тело - совокупность огромного числа атомов (ядер и электронов), свойства и взаимодействие которых между собой и с внешними полями обуславливает все бесконечное разнообразие свойств и поведения твердых тел. Задача теории твердых тел - описание и объяснение свойств и поведения твердых тел исходя из элементарных свойств и законов взаимодействия составляющих его частиц, то есть на атомном уровне. В этом сущность микроскопического подхода.

Законы, управляющие атомами и электронами, - это законы квантовой механики, а в силу чудовищной многочисленности частиц в твердом теле также и статистические законы. В силу этих причин все расчетные методы ФТТ являются приближенными, хотя эта “деталь” не меняет картины в целом.

Раздел физики, изучающий свойства твердых тел и жидкостей и происходящие в них явления, называется физикой конденсированных тел или физикой твердого тела и в настоящее время(повторим еще раз) представляет собой одну из основных областей физических исследований.

1. ОСНОВЫ ЗОННОЙ ТЕОРИИ ТВЕРДЫХ ТЕЛ.

Классическую электронная теория проводимости говорит о том, что в металлах существуют свободные электроны. Что такое свободный электрон с точки зрения квантовой теории?

Естественно , что электрон в металле согласно законам квантовой механики должен описываться волновой функцией и занимать определенный энергетический уровень. Допустим, что электрон перешел на более высокий энергетический уровень. Можно ожидать, что его волновая функция станет более размытой. Но при этом электрон окажется ближе к соседним атомам. Поскольку остовы этих атомов обладают положительным зарядом и притягивают электрон, то они будут еще больше размывать электронную волновую функцию. В результате такого эффекта волновая функция окажется равномерно размытой по всему кристаллу( с некоторыми сгущениями вблизи каждого притягивающего атомного остова). Кристаллы с таким типом связи называют металлами. Металлическая связь возникает, когда атомы сближаются на расстояния, меньшее размеров облака внешних электронов. В конечном итоге волновая функция каждого из внешних электронов равномерно распределяется по всему кристаллу.

Для построения простой квантовомеханической теории поведения электронов в металлах Зоммерфельд предположил, что электроны перемещаются в металле совершенно свободно, но покинуть его не могут. Первое предположение является конечно сильным упрощением. Как бы свободны не были электроны в реальном металле, они всегда “чувствуют” на себе воздействие оставленных ими ионов. Условие, что электроны не покидают металл по существу означает, что движение каждого электрона ограничено в пространстве и требуется совершить некоторую работу, чтобы вырвать электрон из металла (так называемая “работа выхода”).

Чтобы лучше описать поведение электронов в твердых телах, мы должны учесть наличие атомов - бывших владельцев электронов. Электроны в металле покидают свои атомы и продолжают движение не в пустом ящике, а в ящике заполненном решеткой положительных ионов. Поскольку каждый ион притягивает каждый электрон, вероятность найти какой -либо электрон вблизи иона несколько больше, чем вдали от него. Если ионы в кристаллической решетке располагаются равномерно, потенциальная энергия электрона должна меняться периодически из-за взаимодействия ионов и электрона. Фактически потенциальная энергия электрона имеет вид расположенных равномерно потенциальных ям. Рассмотрим к чему это может привести.

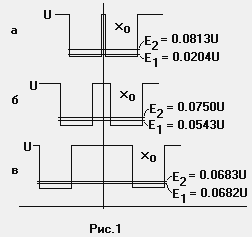
В качестве первого примера рассмотрим две одномерные прямоугольные ямы глубиной Uo и шириной хо. Они соответствуют эффекту, который дают два последовательно расположенных атомных остова. Покажем, что первоначальный энергетический уровень основного состояния, существовавший в каждой из ям, превратится в “зону” с двумя значениями энергии. В случае же “n” последовательно расположенных прямоугольных ям основному состоянию будет соответствовать зона, содержащая “n” энергетических уровней.

Энергии уровней в отдельной прямоугольной яме можно записать в виде ( для простоты возьмем выражение для бесконечной ямы - это конечно приближение серьезное, но качественно результат не изменится , в то же время на рис. 1 показаны результаты для потенциальной ямы конечной глубины U):

En = n2p2h2/L22m , (1)

где L - ширина ямы, h = 1.05×10-34 - постоянная Планка.

Если теперь (см.рис.1а) соединить две ямы в одну, но с удвоенной шириной (L=2xo), то мы получим:

En = n2p2h2/4L22m

Е1 » p2h2/4L22m и E2» p2h2/L22m

На рис.1б яма “двойной ширины поделена на две соседствующие одинаковые ямы. Заметим, что энергии, отвечающие волновым функциям y1 и y2, сблизились друг с другом. На рис. 1в обе ямы раздвинуты настолько, что практически

Е1 » E2 » p2h2/L22m

Таким образом мы показали, что при сближении двух ям уровни энергии раздвигаются. Состояние с наинизшей энергией в случае отдельной ямы превращается в два состояния с различными энергиями в случае двух ям, причем чем меньше расстояние между ямами, тем сильнее раздвинуты соответствующие уровни.