число степеней свободы точки равно 0.

Если одна координата может быть переменной, например (),

возникает одна степень свободы. Точка может иметь любые значения у — от 0 до 1. Следовательно, запись () отвечает геометриче­скому месту бесконечно большого количества точек, в данном случае прямой линии, параллельной оси у.

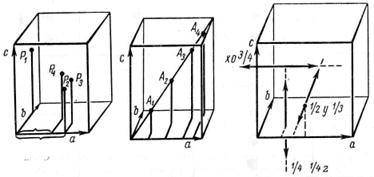Рис. 16. Координаты точек и линий в элементарной ячейке

2 .

На том же рис. 16 показаны прямые (); (x0);().

Прямые (x00) (0y0) (00x) совпадают с осями а, b, с.

I, А, В, С и F-ячейкам отвечают координаты точек:

I:(000, ); А : (000, 0) ; В (000,0);

С:(000, 0); F(000,0,0,0).

При описании координат точек во избежание повторного выписы­вания меняющихся местами одних и тех же дробей, характеризующих позиции нескольких точек, иногда приводят координаты одной из них, после чего ставится знак. Например, положение точек в F-гранецентрированной ячейке записывается так:

(000, 0,).

3. СИММЕТРИЯ ЭЛЕМЕНТАРНОЙ ЯЧЕЙКИ.

О РАСЧЕТАХ РАССТОЯНИЙ И ОБЪЕМОВ

В ПРОСТРАНСТВЕННЫХ РЕШЕТКАХ

Симметрия элементарной ячейки определяется следующими фак­торами:

а) метрикой элементарной ячейки (т. е. осевыми отрезками а, b, с и углами );

б) расположением центров тяжести точек (частиц) в элементарной ячейке;

в) собственной симметрией точек;

г) их ориентировкой по отношению к осям элементарных ячеек.

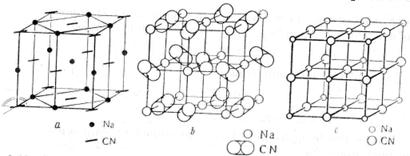Рис. 17. Влияние собственной симметрии и ориентировки СN-групп на струк­туру и вид симметрии NаСN:

a- ромбическая (низкотемпературная) {показаны большие оси эллипсоидов СN-ионов}; b — кубическая(вид симметрии Т); с — кубическая,вид симметрии O

Например, у цианидов типа NaCN при низких температурах ган­тельные сигарообразные группы СN ориентируются перпендикулярно оси с, так что аbс, = 90°, элементарная ячейка NаСN ромбическая. Вид симметрии (рис. 17, а). Структура — деформированный тип NаС1. При более высоких температурах группы СN статистически равномерно ориентированы по отношению ковсем трем осям так, что а =b= с, и вид симметрии Т; куби­ческая структура пирита FеS2, т. е. тоже деформированный тип структуры NаС1, но симметрия элементарной ячейки уже значитель­но выше (рис. 17, b). Наконец, при высоких температурах группа СN, вращаясь, приобретает шаровую симметрию и -NаСN образует структуру типа NаС1 (рис. 17, с), вид симметрии Оh. Условия фазо­вых переходов неясны из-за недостатка надежных данных.

О расчетах расстояний и объемов в пространственных решетках. Расстояния между двумя точками в пространственной решетке могут быть охарактеризованы вектором [см. уравнение (3)]

(5)

Если за нулевую точку выбрана некоторая идентичная точка (узел) и m , п и р — целые числа, уравнение (5) определяет, как мы знаем, положения других идентичных точек; если же m , п и р — правильные дроби, то уравнение (5) определяет положения точки внутри эле­ментарной ячейки. Для определения абсолютной величины расстоя­ния от точки (000) до любой (тпр) внутри элементарной ячейки надо умножить вектор скалярно на самого себя, причем получим функцию =f(тпр) в виде квадратичной формы, где а, b, c - скаляры соответствующих векторов (периоды идентичности)

(6)

С повышением симметрии решетки формула (6) упрощается. Для ромбической сингонии (,= 0)

(7)

Для кубической сингонии (a=b=c, )

,

. (8) Квадратичная функция (6) характеризует сингонию простран­ственной решетки.

Нетрудно видеть, что уравнение (8) является частным случаем известного уравнения аналитической геометрии

(9) для пространства в декартовых координатах, где х1у1z1 — координаты первой, х2у2z2 — координаты второй точки; уравнение (9) превра­щается в (8), при для точек (000) и х1=mа, у1 = nа, z1 = ра. Оно пригодно и для тетрагональных и ромбиче­ских структур с учетом (7).

Так, например, для точек P() и P(000) в кубической элементарной ячейке