Пространственная решетка и трансляционные группы
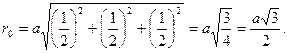
Это расстояние равно половине объемной диагонали куба. Для точек P![]() (3/4 1/2 3/4) и P2 (1/4 ½ 1/2)
(3/4 1/2 3/4) и P2 (1/4 ½ 1/2)
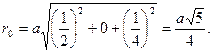
В кристаллохимии и рентгеновском анализе принято выражать межплоскостные расстояния как функцию (hkl).
В общем случае получается довольно сложная зависимость, которая сильно упрощается в случае кубической сингонии.
 |  | ||
|
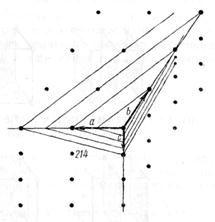
Рис. 19. Плоскости (214) в кубической решетке |
Рис. 18. Плоскости с разными (hk0) в кубической решетке (параллельные оси z)
Начнем с плоскостей, параллельных оси с. Соответствующий индекс ![]() = 0. Пересекая плоскость, образованную трансляционными векторами
= 0. Пересекая плоскость, образованную трансляционными векторами ![]() и
и ![]() , они оставляют следы пересечения, показанные для некоторых плоскостей на рис. 18. Сформулируем общее правило: значения индексов определяются числом плоскостей, пересекаемых соответствующим трансляционным вектором от одного узла решетки до другого, идентичного.
, они оставляют следы пересечения, показанные для некоторых плоскостей на рис. 18. Сформулируем общее правило: значения индексов определяются числом плоскостей, пересекаемых соответствующим трансляционным вектором от одного узла решетки до другого, идентичного.
Как применять это несложное правило, видно из рис. 18. Этот раздел важен также для правильного понимания выводов из уравнения Вульфа—Брэгга: ![]() .
.
Очевидно, что межплоскостное расстояние ![]() вдвое больше расстояния
вдвое больше расстояния ![]() , втрое больше межплоскостного расстояния
, втрое больше межплоскостного расстояния
![]() и т. д. Следовательно, расстояние
и т. д. Следовательно, расстояние ![]() вдвое больше расстояния
вдвое больше расстояния ![]() и вчетверо больше межплоскостного расстояния
и вчетверо больше межплоскостного расстояния ![]() .
.
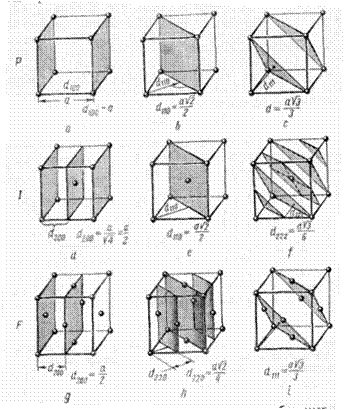 |
Рис. 20. Наибольшие расстояния ![]() в кубических Р-, Т- и F-решетках
в кубических Р-, Т- и F-решетках
В случае кубической сингонии величина межплоскостного расстояния, выраженная в единицах периода идентичности a, как функция (hkl) выражается уравнением
![]() (10)
(10)
или
![]() (11)
(11)
и, например,
![]()
Из(7) и (1.11) вытекает важный вывод: с увеличением ![]() межплоскостные расстояния уменьшаются.
межплоскостные расстояния уменьшаются.
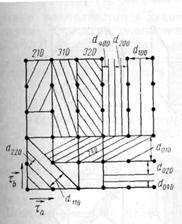
На рис. 20 представлены межплоскостные расстояния в кубических Р-, I и F-решетках. Из рисунка видно, что в случае Р-решетки наибольшим является расстояние d100. На основании формулы (11) это же межплоскостное расстояние должно было бы быть наибольшим реальным и для объемноцентрированной I- и для гранецентрированной F-решетки. Однако из рис. 20 видно, что это не совсем так. В случае I-решетки в центре элементарной ячейки имеются атомы, т. е. параллельно плоскостям (100) проходят плоскости (200), расстояния между которыми равны ![]() . Это же вытекает и из (11). Таким образом, наибольшими в данном случае являются расстояния d110. В случае F-решетки атомы лежат не только в плоскостях (200), но и (220). В этом случае наибольшим реальным является расстояние d111, следующим оказывается d200 и еще меньше d220. Естественно, это следует и из (11).
. Это же вытекает и из (11). Таким образом, наибольшими в данном случае являются расстояния d110. В случае F-решетки атомы лежат не только в плоскостях (200), но и (220). В этом случае наибольшим реальным является расстояние d111, следующим оказывается d200 и еще меньше d220. Естественно, это следует и из (11).
4. ОБ ОСНОВНЫХ ТИПАХ ПРОСТРАНСТВЕННЫХ РЕШЕТОК. О ПРОСТРАНСТВЕННЫХ ГРУППАХ
В настоящее время известны многие сотни различных структур. Здесь мы остановимся только на важнейших, представляющих либо теоретический, либо практический интерес в кристаллохимии полупроводников.
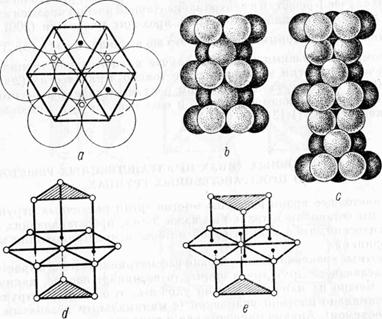
Плотные упаковки.Если условно рассматривать атомы в кристалле как касающиеся друг друга шары, то возникает вопрос, каким образом можно их наиболее плотно уложить, т. е. создать структуру с максимально плотной упаковкой (с минимальным незанятым атомами объемом). Анализ приводит нас к выводу, что возможны только две исходные плотнейшие упаковки: кубическая и гексагональная. С ними мы уже поверхностно знакомы (рис. 11, е и d). Рассмотрим их подробнее.
Существует только одно решение задачи плотнейшей упаковки шаров одинакового диаметра в одной плоскости: вокруг центрального шара должно быть расположено 6 шаров в вершинах правильного шестиугольника (рис. 21, a). Если следующий ряд укладывать на первый так, чтобы центры тяжести шаров приходились друг над другом, плотная упаковка не получится. Для ее получения надо укладывать шары второго ряда в промежутки между шарами первого ряда (рис. 21, а — пунктир). Центры тяжести шаров второго ряда показаны черными кружками. До сих пор упаковка по кубическому и гексагональному закону совпадает.
Если теперь шары третьего ряда уложить так, что их центры тяжести придутся над центрами тяжести шаров первого ряда (рис. 21, b), получится плотнейшая гексагональная упаковка. Если шары третьего ряда уложить так, что их центры тяжести придутся над позициями, отмеченными белыми кружками на рис. 21, а, а шары четвертого ряда — над шарами первого ряда, то получим плотнейшую кубическую упаковку (рис. 21, с).
|
|