1.

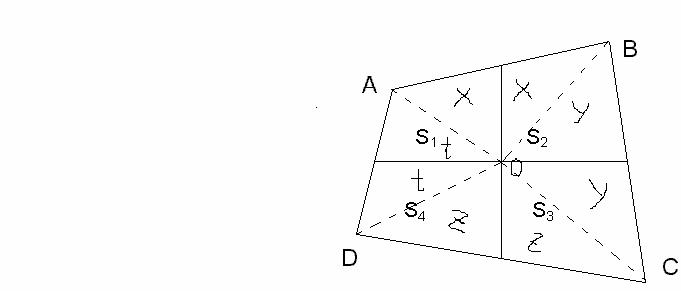
Рассмотрим выпуклый четырёхугольник. Две диагонали делят его на четыре треугольника. Обозначим их площади (в порядке обхода) S1, S2, S3, S4. Тогда произведения площадей «крест-накрест» равны: S1S3 = S2S4. (Рис. 1.)

Рис. 1. S1 m n S4 α S2 p k S3

Это легко доказать, обозначив отрезки диагоналей m, n, k, p, зная, что синусы всех четырёх углов при пересечении диагоналей равны синусу одного из них sin α:

S1 = mn sin α,

S2 = nk sin α,

S3 = kp sin α,

S4 = pm sin α, откуда получаем требуемое равенство.

2.

Попробуем разделить выпуклый четырёхугольник на четыре четырёхугольника средними линиями. Средней линией четырёхугольника будем называть отрезок, соединяющий середины противоположных сторон. (Рис. 2.)

Обозначим площади четырёхугольников как S1, S2, S3, S4 .

Соединим точку пересечения средних линий О с каждой вершиной четырёхугольника. В получившихся треугольниках ОАВ, ОВС, ОСD, ODA отрезки средних линий будут являться медианами. Как известно, медиана треугольника делит его площадь пополам. Пусть площади указанных треугольников будут соответственно x, y, z, t. Тогда S1 + S3 = x + y + z + t, S2 + S4 = x + y + z + t, или

S1 + S3 = S2 + S4. (•)

То есть, суммы площадей противоположных четырёхугольников «крест-накрест» равны.

Рассмотрим ещё раз тот же четырёхугольник, соединив середины сторон M, N, K, L последовательно (рис. 3.).

Поскольку ML является средней линией в треугольнике ABD, то она отсекает треугольник ALM, подобный ABD и составляющий по площади 1/4 часть площади ABD. Аналогично треугольник CNK. Значит, в сумме площади треугольников AML и CNK составляют 1/4 площади четырёхугольника ABCD. Аналогично 1/4 площади четырёхугольника ABCD составляет сумма площадей треугольников MBN и DKL. Следовательно, сумма площадей «угловых» треугольников составляет 1/4 + 1/4 = 1/2 площади четырёхугольника ABCD – половину. Но тогда на долю внутреннего четырёхугольника MNKL также остаётся половина. В результате имеем: S1 + S2 + S3 + S4 = S0.

Заметим, что средние линии четырёхугольника делят друг друга пополам, как диагонали параллелограмма MNKL (ML – средняя линия в треугольнике ABD, параллельна BD и равна её половине, то же самое NK в треугольнике BDC).

3.

Рассмотрим теперь выпуклый четырёхугольник с линиями, делящими противоположные стороны на три равные части (см. рис. 5.) и поставим задачу:

Рис. 5. В А D C

в каком отношении нахо- дятся площади внутренних четырёхугольников?

Для этого решим сначала упрощенную задачу: какую часть площади четырёх- угольника составляет средняя часть, если про- вести только две линии, делящие лишь одну пару противоположных сторон на три равные части

(рис. 6.).

Рис. 6. В N M Q А P hA hM hB D K L C