Пусть эти прямые делят четырёхугольник в каждом направлении на «n» полосок (т.е. n×n клеток), и пусть NL отделяет m полосок слева, а TR – k полосок снизу (рис. 10.).

Пусть далее вектор таков, что его модуль равен ּDС , т.е.

Аналогично Будем считать векторы и базисными. Для того, чтобы четырёхугольник ABCD был однозначно определён, введём ещё вектор , равный = α + β. Здесь α и β таковы, что четырёхугольник ABCD невырожденный и выпуклый. Понятно, что Очевидно также, что

Вычислим следующие векторы:

Поскольку векторы коллинеарны, а также коллинеарны векторы и так как то где х и у – некоторые коэффициенты, найдя которые, мы узнаем, в каком отношении делятся отрезки NL и TR точкой их пересечения О.

Распишем последнее равенство через базисные векторы:

x(n – k + αk) + βkx + y(m – αm) − y(βm + n) = m − k, или

(x(n – k + αk) + y(m – αm) – m) + (βkx − y(βm + n) + k) = 0.

Так как векторы и неколлинеарны и ненулевые, то последнее равенство возможно тогда и только тогда, когда оба коэффициента перед этими векторами одновременно равны нулю:

(n – k + αk)х + (m – αm)у – m = 0,

βkx − (βm + n)у + k = 0.

Решим эту систему относительно х и у.

Из второго уравнения у = Подставив в первое, получим:

х = Из предыдущего у =

Это означает, что TR делится точкой О так же, как АВ точкой N, и DC точкой L, и что NL делится так же, как AD и ВС.

Итак, доказано, что если прямые делят каждую пару противоположных сторон четырёхугольника на «n» равных частей, то отрезок каждой прямой, находящийся внутри четырёхугольника, делится на «n» равных частей.

5.

Рис. 11. В А а a + d a + 2d a + q a + d + q a + 2d + q D a + 2q a + 2q + d a + 2d + 2q C

Вернёмся к четырёхуголь- нику, разделённому че- тырьмя прямыми так, что- бы противоположные сто- роны делились на равные части (рис. 11). Как мы теперь знаем, каждый из отрезков этих прямых, заключённый внутри четы-рёхугольника, делится на равные части. А значит, площади трёх клеточек каждой горизонтальной, а также каждой вертикальной полосы составляют арифметическую прогрессию. Таким образом, если площадь левой верхней клеточки равна «а», то справа от неё будет клеточка с площадью а + d, а ещё правее a + 2d. Ниже клеточки с площадью «а» будет клеточка с площадью a + q, а ещё ниже a + 2q. Площадь центральной клеточки можно выразить из формулы (•), рассматривая четыре смежные клеточки как четырёх-угольник со средними линиями (суммы площадей «крест-накрест» равны). Это будет a + d + q. По той же схеме или по правилу арифметической прогрессии выражаем остальные площади.

Замечаем, что в каждом горизонтальном ряду площади составляют прогрессию с одной и той же разностью «d», а в каждом вертикальном – с разностью «q».

Арифметические прогрессии составляют также площади по диагоналям: по одной с разностью d + q, по другой d – q.

Заметим также, что суммы площадей противоположных – угловых – клеточек равны (2a + 2d + 2q). Равны также площади противо- положных – не угловых – клеточек (тоже 2a + 2d + 2q). Сумма площадей угловых клеточек равна сумме площадей не угловых (центральная клеточка не в счёт). Что касается центральной клеточки, то её площадь составляет 1/9 площади всего четырёх- угольника.

6.

Если разделить четырёхугольник прямыми так, чтобы каждая пара противоположных сторон разделилась на «n» равных частей, то, как мы знаем, каждый отрезок прямой, заключённый внутри четырёхугольника, разделится на «n» равных частей. Рассмотрим одну из горизонтальных или вертикальных полос, разбитых на «n» клеточек (рис. 12).

Рис. 12. a a + d a+2d a+3d

Площади первых трёх клеточек образуют арифметическую прогрессию. Площади второй, третьей и чет- вёртой – тоже. Таким образом, все четыре площади образуют одну арифметическую прогрессию, так как отличаются на одну и ту же величину. Далее третья, четвёртая и пятая клеточки и т. д. – площади всех клеточек будут членами этой прогрессии.

Аналогично, как в предыдущем случае , убеждаемся, что все «горизонтальные» прогрессии имеют одну и ту же разность, а все «вертикальные» - также одну и ту же (не всегда совпадающую с первой). Одинаковые разности и у прогрессий в направлении диагоналей.

Пусть четырёхугольник разбит известными нам прямыми на n×n клеточек, где n – чётное (рис. 13).

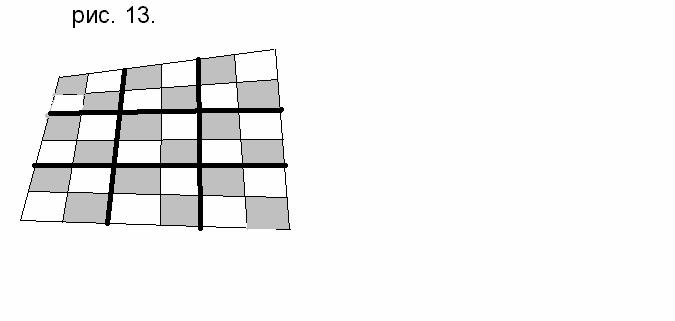
Раскрасим клеточки в шахматном порядке и разобъём их на четвёрки, что можно сделать, т. к. n – чётно. Внутри каждой четвёрки выполняется правило суммы «крест-накрест». Значит, во всём четырёхугольнике сумма площадей чёрных клеточек равна сумме площадей белых.

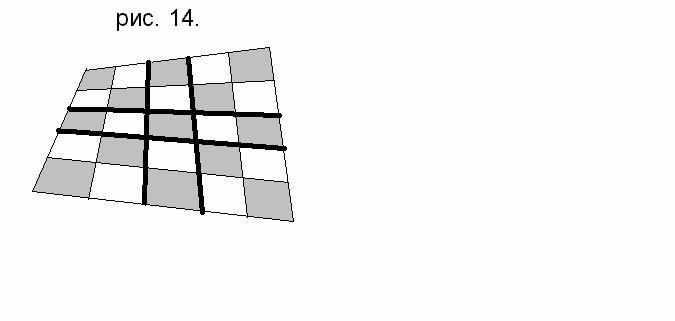
Пусть число клеток четырёхугольника нечётно, а именно(4n + 1)×(4n + 1).

В звене с к