Иррациональные уравнения и неравенства

Рефераты >> Математика >> Иррациональные уравнения и неравенства

x = -пост. корень 0

Ответ: 1. x = 1,

1 = 1

· Иррациональные логарифмические уравнения:

а) Решить уравнение lg3 + 0,5lg(x – 28) = lg

Решение.

lg3 + 0,5lg(x – 28) = lg,

lg(3 = lg,

Учитывая ОДЗ, данное уравнение равносильно системе:

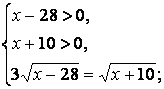
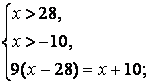
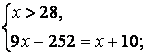
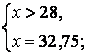
Ответ: 32,75

б) Решить уравнение

Решение.

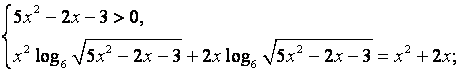
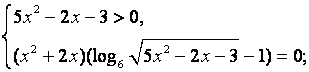
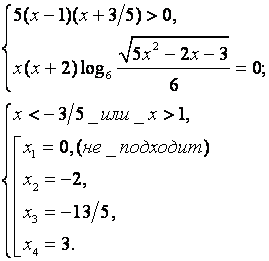
Ответ: ; – 2; 3.

IV. Иррациональные неравенства

Неравенства называются иррациональными, если его неизвестное входит под знак корня (радикала).

Иррациональное неравенство вида равносильно системе неравенств:

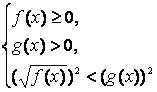
Иррациональное неравенство вида равносильно совокуп-ности двух систем неравенств:

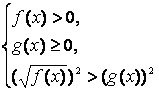и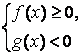

Решение иррациональных неравенств стандартного вида:

а) Решить неравенство

Решение.

Данное неравенство равносильно системе неравенств:

+ – +

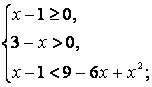
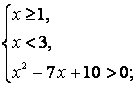
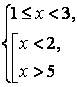Ответ: [1; 2). 1 3 x

б) Решить неравенство

Решение.

Данное неравенство равносильно двум системам неравенств:

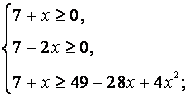
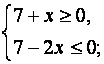
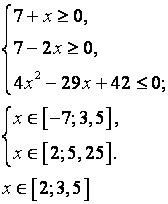
Ответ:

в) Решить неравенство

Решение.

Данное неравенство равносильно системе неравенств:

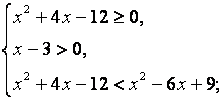
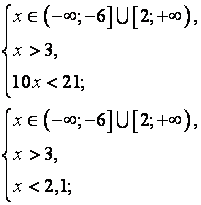
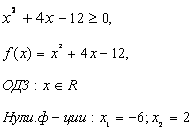
Ответ: нет решений

Решение иррациональных неравенств нестандартного вида:

а) Решить неравенство

Решение.

Данное неравенство равносильно системе неравенств:

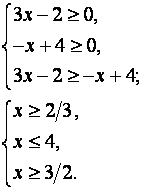
Ответ:

б) Решить неравенство

Решение.

Данное неравенство равносильно системе неравенств:

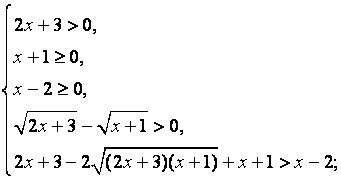
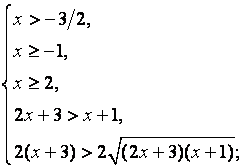
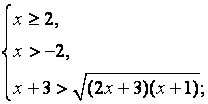
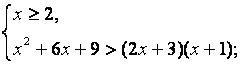
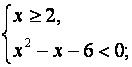
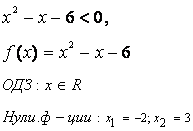
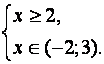
Ответ:

· Решение иррациональных неравенств с помощью правила знаков при умножении и делении:

а) Решить неравенство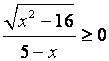

Решение.

Учитывая то, что и правило знаков при делении данное неравенство равносильно системе неравенств: