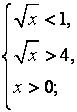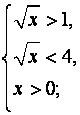Иррациональные уравнения и неравенстваРефераты >> Математика >> Иррациональные уравнения и неравенства
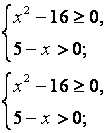

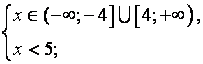
Ответ: ![]()
б) Решить неравенство (2x – 5)![]()
Решение.
(2x – 5)![]()
Учитывая то, что ![]() и правило знаков при делении данное неравенство равносильно системе неравенств:
и правило знаков при делении данное неравенство равносильно системе неравенств:
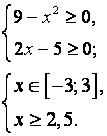
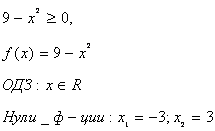
Ответ: ![]()
· Решение иррациональных неравенств способом группировки:
Решить неравенство ![]()
Решение.
![]() ,
,
![]() сгруппируем по два слагаемых
сгруппируем по два слагаемых
![]()
![]()
![]() вынесем общий множитель за скобку
вынесем общий множитель за скобку
![]() учитывая, что
учитывая, что ![]() > 0 и правило знаков при умножении данное неравенство равносильно системе неравенств:
> 0 и правило знаков при умножении данное неравенство равносильно системе неравенств:
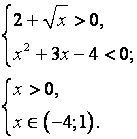

Ответ: ![]() ( 0; 1 )
( 0; 1 )
· Иррациональное неравенство, содержащее два знака иррациональности:
Решить неравенство ![]()
Решение.
![]()
Данное неравенство равносильно системе неравенств:

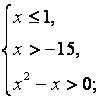

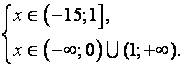
Ответ: ![]()
· Решение иррациональных неравенств заменой:
Решить неравенство 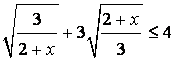
Решение.
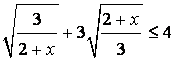
Пусть 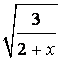 = t, тогда
= t, тогда 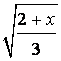 =
= ![]() , t > 0
, t > 0
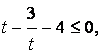
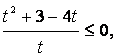
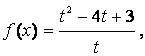
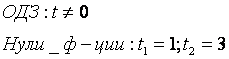
![]()
Сделаем обратную замену:
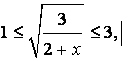 возведем в квадрат обе части неравенства
возведем в квадрат обе части неравенства
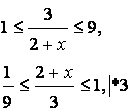
![]()
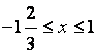
Ответ: 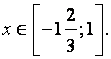
Решение иррациональных неравенств смешанного вида:
· Иррациональные показательные неравенства:
а) Решить неравенство ![]()
Решение.
![]() ,
,
![]() т.к. y = 0,8t
т.к. y = 0,8t ![]() , то
, то
0,5x(x – 3) < 2,
0,5x2 – 1,5x – 2 < 0,
x2 – 3x – 4 < 0,
f(x) = x2 – 3x – 4,
ОДЗ![]() , + – +
, + – +
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Нули функции: x1 = 4; x2 = – 1. –1 4 x
Нули функции: x1 = 4; x2 = – 1. –1 4 x
Ответ: х![]()
б) Решить неравенство 4![]() – 2
– 2![]() < 2
< 2![]() – 32
– 32
Решение.
4![]() – 2
– 2![]() < 2
< 2![]() – 32, ОДЗ: x > 0
– 32, ОДЗ: x > 0
2![]() – 2
– 2![]()
![]() 2 < 2
2 < 2![]()
![]() 24 – 25, выполним группировку слагаемых
24 – 25, выполним группировку слагаемых
2![]() (2
(2![]() – 2) – 24(2
– 2) – 24(2![]() –2) < 0,
–2) < 0,
(2![]() – 2)
– 2) ![]() (2
(2![]() – 24) < 0, учитывая правило знаков и ОДЗ данное неравенство равносильно 2-м системам:
– 24) < 0, учитывая правило знаков и ОДЗ данное неравенство равносильно 2-м системам:
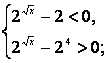 или
или 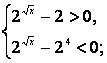
![]()
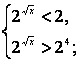 т.к. y = 2t
т.к. y = 2t ![]() , то
, то 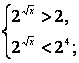 т.к. y = 2t
т.к. y = 2t ![]() , то
, то