Независимую переменную х называют также аргументом функции. Число у, соответствующее числу х, называют значением функции f в точке х и обозначают f(x).

Функцию можно задать тремя способами: аналитический, табличный, графический.

Аналитический – с помощью формул.

Табличный – с помощью таблиц, где можно указать значения функции, однако лишь для конечного набора значений аргумента.

Графический способ задания функции очень удобен: он дает возможность наглядно представить свойства функции.

Графиком функции f называют множество всех точек (х;у) координатной плоскости, где y=f(x), а х «пробегает» всю область определения функции f.

Пример 1. Найти область определения функции y=lg (2x-3)

y=lg(2x-3)

D(y): 2x-3>0

2x>3

x>1,5

Ответ: D(y)=(1,5; +∞ ).

Одним из понятий для исследования функции является нули функции.

Нули функции – это точки, в которых функция принимает значение нуля.

Пример 2. Найти нули функции y=x2-5x.

y=x2-5x

D(y)=R

По определению :

y=0, тогда

x2-5x=0

x(x-5)=0

x=0 или x=5

Ответ: нулями функции являются точки x=0 и х=5.

Пример 3. Найти нули функции y=4x-8

y=4x-8

D(y)=R

По определению:

у=0, тогда

4х-8=0

4x=8

x=2

Ответ: нулями этой функции является точка х=2.

2.2. Виды функций (четные, нечетные, общего вида, периодические функции).

Рассмотрим функции, области определения которых симметричны относительно начала координат, то есть для любого х из области определения число (-х) также принадлежит области определения. Среди таких функций выделяют четные и нечетные.

Определение: Функция f называется четной, если для любого х из ее области определения f(-x)=f(x).

График четной функции симметричен относительно оси ординат.

Пример 4. Определить вид функции y=2cos2x.

y=2cos2x, D(y)=R

y(-x)=2cos2(-x)=-2cos2x=2cos2x=y(x) – четная.

Пример 5. Определить вид функции y=x4-2x2+2.

y=x4-2x2+2, D(y)=R.

y(-x)=(-x)4-2(-x)2+2=x4-2x2+2=y(x) – четная.

Определение:Функция f называется нечетной, если для любого х из ее области определения f(-x)=-f(x).

График нечетной функции симметричен относительно начала координат.

Пример 6. Определить вид функции y=2sin2x.

y=2sin2x, D(y)=R

y(-x)=2sin2(-x)=-2sin2x=-y(x) – нечетная.

Пример 7. Определить вид функции y=3x+1/3x.

y=3x+1/3x

y(-x)=3(-x)+1/3(-x)=-3x-1/3x=-(3x+1/3x)=-y(x) – нечетная.

Пример 4. Пример 5.

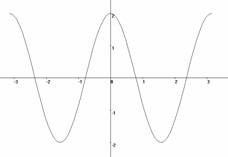
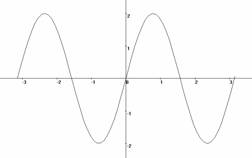
Определение: Функцию f называют периодической с периодом Т≠ 0, если для любого х из области определения значения этой функции в точках х, х-Т и х+Т равны, то есть f(x+T)=f(x)=f(x-T).

Пример 8. Определить период функции y=cos2x.

cos2x=cos2(x+T)=cos(2x+2T), где 2T=2π, т.е. Т=π.

Для построения графика периодической функции с периодом Т достаточно провести построение на отрезке длиной Т и затем полученный график параллельно перенести на расстояния nT вправо и влево вдоль оси Ох.

Пример 9. Построить график периодической функции f(x)=sin2x.

f(x)=sin2x,

sin2x=sin2(x+T)=sin(2x+2T), где 2Т=2π, т.е. Т=π.

2.3. Возрастание и убывание функций. Экстремумы.

Также к свойствам функции относятся возрастание и убывание функции, экстремумы.

Функция f возрастает на множестве Р, если для любых х1 и х2 из множества Р, таких, что х2>х1 , выполнено неравенство f(x2)>f(x1).

Функция f убывает на множестве Р, если для любых х1 и х2 из множества Р, таких, что х2>х1 , выполнено неравенство f(x2)<f(x1).

Иными словами, функция f называется возрастающей на множестве Р, если большему значению аргумента из этого множества соответствует большее значение функции. Функция f называется убывающей на множестве Р, если большему значению аргумента соответствует меньшее значение функции.

При построении графиков конкретных функций полезно предварительно найти точки минимума (xmin) и максимума (xmax).

Точка х0 называется точкой максимума функции f , если для всех х из некоторой окрестности х0 выполнено неравенство f(x) ≤f(x0).

Точка х0 называется точкой минимума функции f , если для всех х из некоторой окрестности х0 выполнено неравенство f(x)≥ f(x0).

Точки минимума и максимума принято называть точками экстремума.

Пример 10. Найти точки экстремума, экстремумы функции y=x2+2x, и указать промежутки возрастания и убывания функции.

y=x2+2x, D(y)=R

y’=(x2+2x)’=2x+2

y’=0, т.е. 2х+2=0

2х=-2

х=-1

Исследуем знак производной справа и слева от крайней точки.

- +

-1

min

x=-2, y’=-4+2<0

x=0, y’=0+2>0

Так как производная меняет свой знак с «-» на «+», то х=-1, это точка минимума функции.

Так как функция непрерывна в точке х=-1, то функция возрастает на [-1;+∞] и убывает на [-∞;-1].

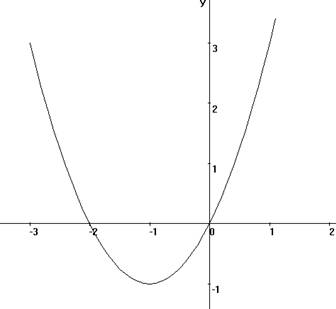
Точки экстремума: xmin= -1

Экстремумы функции: ymin=y(-1)=1-2= -1

Глава III. Исследование функций.

3.1. Общая схема исследования функций.

Исследуя функцию, нужно знать общую схему исследования:

1) D(y) – область определения (область изменения переменной х)

2) E(y) – область значения х (область изменения переменной у)

3) Вид функции: четная, нечетная, периодическая или функция общего вида.

4) Точки пересечения графика функции с осями Охи Оу (по возможности).

5) Промежутки знакопостоянства:

а) функция принимает положительное значение : f(x)>0

б) отрицательное значение : f(x)<0.

6) Промежутки монотонности функции:

а) возрастания;

б) убывания;

в) постоянства ( f=const).

7) Точки экстремума (точки минимума и максимума)

8) Экстремумы функции (значение функции в точках минимума и максимума)

9) Дополнительные точки.

Они могут быть взяты для того, чтобы более точно построить график функции.

Следует заметить, что экстремумы функции f не всегда совпадают с наибольшим и наименьшим значением функции.

3.2. Признак возрастания и убывания функций.

Если строить график функции по каким-либо произвольно выбранным его точкам, соединяя их плавной линией, то даже при очень большом числе случайно выбранных точек может оказаться, что построенный таким образом график будет сильно отличаться от графика заданной функции.

Если при исследовании функции использовать производную и найти так называемые «опорные» точки, т.е. точки разрыва, точки максимума и минимума, промежутки монотонности функции, то даже при небольшом числе таких «опорных» точек мы получим правильное представление о графике функции.