2) Аналогично, возрастающей будет и фукнкция

f(x) = x – sin x,

ибо ее производная

f¢(x) = 1 – cos x

не отрицательна, обращаясь в нуль для значений x = 2kp (k=0, 1,

-1,2,-2…).

3. Максимумы и минимумы; необходимые условия.

Если функция f(x), определена и непрерывна в промежутке [a, b], не является в нем монотонной, то найдутся такие части [a, b], промежутка [a, b], в которой наибольшее и наименьшее значение достигается функцией во внутренней точке, т. е. между a и b. На графике функции (рис. 2) таким промежуткам соответствуют характерные горбы или впадины.

Рис. 2

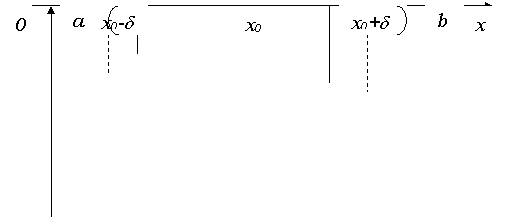Говорят, что функция f(x) имеет в точке x0 максимум (или минимум), если эту точку можно окружить такой окрестностью (x0 - d, x0 + d), содержащейся в промежутке, где задана функция, что для всех выполняется неравенство

f(x) £ f(x0) (или f(x) ³ f(x0)).

Иными словами, точка x0 доставляет функции f(x) максимум (минимум), если значение f(x0) оказывается наибольшим (наименьшим) из значений, принимаемых функцией в некоторой (хотя бы малой) окрестности этой точки. Отметим, что самое определение максимума (минимума) предполагает, что функция задана по обе стороны от точки x0.

Если существует такая окрестность, в пределах которой (при x ¹ x) выполняется строгое неравенство

f(x) < f(x0) (или f(x) > f(x0)).

То говорят, что функция имеет в точке x0 собственный максимум (минимум) в противном случае – несобственный.

Если функция имеет максимумы в точках x0 и x1, то, применяя к промежутку [x0, x1] вторую теорему Вейерштрасса, видим, что наименьшего своего значения в этом промежутке функция достигает в некоторой точке x2 между x0 и x1 и имеет там минимум. Аналогично, между двумя минимумами непременно найдется максимум. В этом простейшем (и на практике - важнейшем) случае, когда функция имеет вообще лишь конечное число максимумов и минимумов, они попросту чередуются.

Экстремум – объединяющий термин максимума и минимума.

Поставим задачу о разыскании всех значений аргумента, доставляющих функции экстремум. При решении ее, основную роль будет играть производная.

Предположим сначала, что для функции f(x) в промежутке (a, b) существует конечная производная. Если в точке x0 функция имеет экстремум, то, применяя к промежутку (x0 - d, x0 + d), о котором была речь выше, теорему Ферма, заключаем, что f¢(x0) = 0: в этом состоит необходимое условие экстремума. Экстремум следует искать только в тех точках, где производная равна нулю; такие точки будем называть стационарными.

Не каждая стационарная точка доставляет функции экстремум: указанное только что необходимое условие не является достаточным. Например, для функции x3 проихводная 3x2 обращается в нуль при x = 0, но в этой точке функция не имеет экстремума: она все время возрастает.

Таким образом, стационарная точка для функции f(x) представляется, так сказать, лишь «подозрительной» по экстремуму подлежит дальнейшему испытанию.

Если расширить класс рассматриваемых функций, допуская, что в отдельных точках нет конечной производной, то не исключена возможность того, что экстремум придется на одну из таких точек. Поэтому их тоже нужно отнести к числу “подозрительных” по экстремуму и подвергнуть испытанию.

4. ПЕРВОЕ ПРАВИЛО

Пусть точка x0 является «подозрительной» по экстремуму для функции f(x).

Предположим, что в некоторой окрестности (x0 - d, x0 + d), этой точки (по крайней мере, для x ¹ x) существует конечная производная f¢(x) и как слева от x0 так и справа от x0 (в отдельности) сохраняет определенный знак. Тогда возможны следующие три случая:

I. f¢(x) > 0 при x < x0 и f¢(x) < 0 при x > x0 т. е. производная f¢(x) при переходе через точку x0 меняет знак плюс на минус. В этом случае, в промежутке [x0 - d, x0], функция f(x) возрастает, а в промежутке [x0 , x0 + d], убывает, так что значение f(x0) будет наибольшим в промежутке [x0 - d, x0 + d], т. е. в точке x0 функция имеет максимум.

II. f¢(x) < 0 при x < x0 и f¢(x) > 0 при x > x0 т. е. производная f¢(x) при переходе через точку x0 меняет знак минус на плюс. В этом случае аналогично убеждаемся, что в точке x0 функция имеет минимум.

III. f¢(x) > 0 как при x < x0 так и при x > x0 либо же f¢(x) < 0 и слева и справа от x0, т. е. при переходе через x0 f¢(x) не меняет знака. Тогда функция либо все время возрастает, либо все время убывает; в любой близости x0 с одной стороны нгайдутся точки x, в которых. f(x) < f(x0), а с другой – точки x, в которых f(x) > f(x0), так что в точке x0 никакого экстремума нет.

Итак, мы получаем первое правило для испытания «подозрительного» значения x0 : подставляя в производную f¢(x) сначала x < x0, а затем x > x0 , устанавливаем знак производной поблизости от точки x0 слева и справа от нее : если при этом производная f¢(x) меняет знак плюс на минус, то налицо максимум, если меняет знак минус на плюс, то – минимум, если же знака не меняет, то экстремума вовсе нет.

Класс функции, к которому применяется это правило.

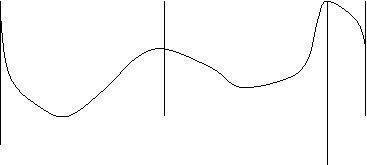
Функция f(x) предполагается непрерывной в промежутке [a, b], и имеющей в нем непрерывную же производную f¢(x), за исключением разве лишь конечного числа точек. В этих точках производная как слева, так и справа стремится к бесконечным пределам, совпадающим по знакам или нет: в первом случае существует двусторонняя бесконечная производная, а во втором – разнящиеся знаками односторонние производные. Допустим, ято обращается в нуль производная лишь тоже в конечном числе точек. Графическая иллюстрация различных возможностей для “подозрительных” по экстремуму точек дана на рис. 3.