4. Обзор различных архитектур нейронных сетей, предназначенных для задач классификации.

Приступая к разработке нейросетевого решения, как правило, сталкиваешься с проблемой выбора оптимальной архитектуры нейронной сети. Так как области применения наиболее известных парадигм пересекаются, то для решения конкретной задачи можно использовать совершенно различные типы нейронных сетей, и при этом результаты могут оказаться одинаковыми. Будет ли та или иная сеть лучше и практичнее, зависит в большинстве случаев от условий задачи. Так что для выбора лучшей приходится проводить многочисленные детальные исследования.

Рассмотрим ряд основных парадигм нейронных сетей, успешно применяемых для решения задачи классификации, одна из постановок которой представлена в данной дипломной работе.

4.1 Нейрон – классификатор.

Простейшим устройством распознавания образов в нейроинформатике является одиночный нейрон (рис. 4.1), превращающий входной вектор признаков в скалярный ответ, зависящий от линейной комбинации входных переменных [1-5, 7,10]:

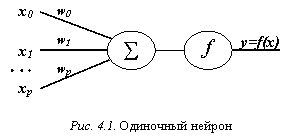Скалярный выход нейрона можно использовать в качестве т.н. дискриминантной функции. Этим термином называют индикатор принадлежности входного вектора к одному из заданных классов, а нейрон соответственно – линейным дискриминатором. Так, если входные вектора могут принадлежать одному из двух классов, можно различить тип входа, например, следующим образом: если f(x) ³ 0, входной вектор принадлежит первому классу, в противном случае – второму. Рассмотрим алгоритм обучения подобной структуры, приняв f(x)ºx.

Итак, в p-мерном пространстве задана обучающая выборка x1,…,xn (первый класс) и y1,…,ym (второй класс). Требуется найти такие p+1-мерный вектор w, что для всех i=1,…,n и j=1,…,m w0+(xi,w)>0 и w0+(yj,w)<0.

Переформулируем задачу, сведя ее к отделению нуля от конечного множества векторов в p+1 - мерном пространстве. Для этого рассмотрим p+1 – мерные векторы zl (l=0, 1,…., n+m):

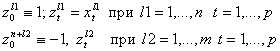В этих обозначениях условия разделения превращаются в систему n+m однотипных неравенств:

В качестве нулевого приближения можно выбрать любой вектор w, например, w=0, или wÍR[-0.5,0.5]. Цикл алгоритма состоит в том, что для всех l = 1,…,n+m проверяется неравенство (zl,w) > 0. Если для данного l £ n+m оно выполнено, переходим к следующем l (либо при l=n+m заканчиваем цикл), если же не выполнено, то модифицируем w по правилу w=w+zl , или w=w+hTzl, где T – номер модификации, а , например.

Когда за весь цикл нет ни одной ошибки ( т.е. модификации w), то решение w найдено, в случае же ошибок полагаем l=1 и снова проходим цикл.

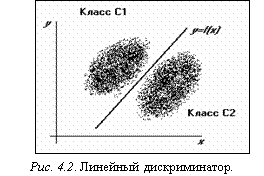
В некоторых простейших случаях линейный дискриминатор – наилучший из возможных, а именно когда оба класса можно точно разделить одной гиперплоскостью, рисунок 4.2 демонстрирует эту ситуацию для плоскости, когда p=2.

4.2 Многослойный персептрон.

Возможности линейного дискриминатора весьма ограничены. Для решения более сложных классификационных задач необходимо усложнить сеть вводя дополнительные (скрытые) слои нейронов, производящих промежуточную предобработку входных данных, таким образом, чтобы выходной нейрон-классификатор получал на свои входы уже линейно-разделимые множества. Такие структуры носят название многослойные персептроны [1-4,7,10] (рис. 1.3).

Легко показать, что, в принципе, всегда можно обойтись одним скрытым слоем, содержащим, достаточно большое число нейронов. Действительно, увеличение скрытого слоя повышает размерность пространства, в котором выходной нейрон производит классификацию, что, соответственно, облегчает его задачу.

Персептроны весьма популярны в нейроинформатике. И это обусловлено, в первую очередь, широким кругом доступных им задач, в том числе и задач классификации, распознавания образов, фильтрации шумов, предсказание временных рядов, и т.д., причем применение именно этой архитектуры в ряде случаев вполне оправдано, с точки зрения эффективности решения задачи.

Рассмотрим какие алгоритмы обучения многослойных сетей разработаны и применяются в настоящее время.[7,10]. В основном все алгоритмы можно разбить на две категории:

· Градиентные алгоритмы;

· Стохастические алгоритмы.

К первой группе относятся те, которые основаны на вычислении производной функции ошибки и корректировке весов в соответствии со значением найденной производной. Каждый дальнейший шаг направлен в сторону антиградиента функции ошибки. Основу всех этих алгоритмов составляет хорошо известный алгоритм обратного распространения ошибки (back propagation error).[1-5,7,10].

,где функция ошибки

Многочисленные модификации, разработанные в последнее время, позволяют существенно повысить эффективность этого алгоритма. Из них наиболее известными являются:

1. Обучение с моментом.[4,7]. Идея метода заключается в добавлении к величине коррекции веса значения пропорционального величине предыдущего изменения этого же весового коэффициента.

2. Автономный градиентный алгоритм (Обучение с автоматическим изменением длины шага h). [10]

3. RPROP (от resilient –эластичный), в котором каждый вес имеет свой адаптивно настраиваемый темп обучения.[4]

4. Методы второго порядка, которые используют не только информацию о градиенте функции ошибки, но и информацию о вторых производных .[3,4,7].

Стохастические методы обучения выполняют псевдослучайные изменения величин весов, сохраняя те изменения, которые ведут к улучшениям характеристик сети. К этой группе алгоритмов относятся такие как

1. Алгоритм поиска в случайном направлении.[10]

2. Больцмановское обучение или (алгоритм имитации отжига). [1]

3. Обучение Коши, как дополнение к Больцмановскому обучению.[1]