Гостиничный рынок Санкт-ПетербургаРефераты >> Статистика >> Гостиничный рынок Санкт-Петербурга
Следовательно, регрессия значима Проверим значимость коэффициента корреляции
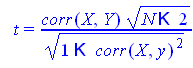
![]()
![]()
поэтому выборочный коэффициент корреляции значимо отличается от нуля.
Средняя ошибка аппроксимации
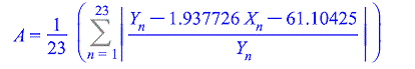
![]()
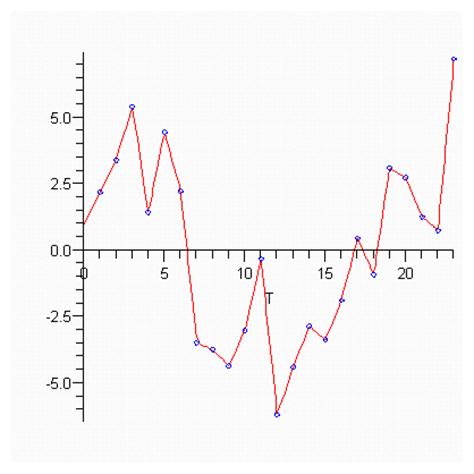
Колеблемость признака
Колеблемость - это отклонения уровней динамического ряда от тренда, т.е. остатки регрессии. Найдем остатки регрессии (т.е. очищаем признак от тренда)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Нарисуем график остатков
Среднее линейное отклонение уровней ряда от тренда описывается показателем
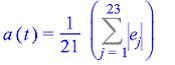
т.е. среднее абсолютное отклонение от тренда равно![]()
Амплитуда колебаний есть разность максимального и минимального отклонения и показывает максимальный разброс отклонений.
![]()
![]()
Степень тесноты связи между последовательностями наблюдаемого временного ряда, сдвинутого относительно друг друга на t единиц может быть определена с помощью коэффициента автокорреляции
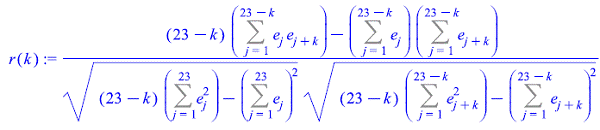
Показатель t служит порядком коэффициента автокорреляции. Для разных t получаем r(t) – автокорреляционную функцию
![]()
![]()
![]()
![]()
а ее график - коррелограмма.
Статистика Дарбина-Уотсона
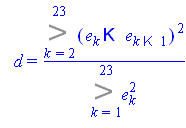
![]()
Попали в зону положительной автокорреляции.
Прогноз
Точечный прогноз для ![]()
![]()
Интервальный прогноз с вероятностью 95%
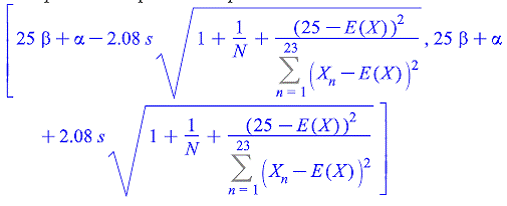
![]() или
или![]()
Выводы: Регрессия оказалась значимо по F статистикам, по t-статистикам. Каждый квартал стоимость увеличивается в среднем на 1,93$. К сожалению, в регрессии присутствует автокорреляция первого порядка.
3.3. Индексный анализ динамики цен
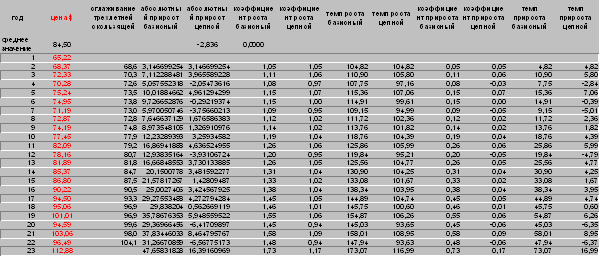
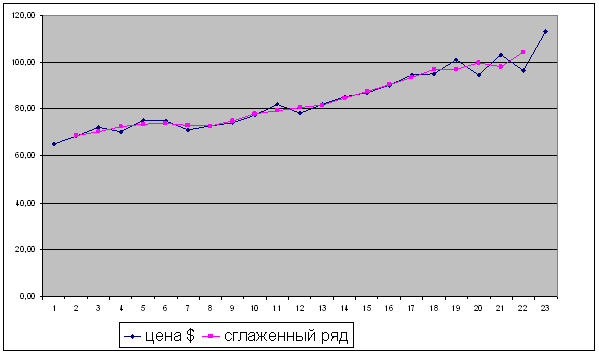
Приведем основные формулы:
Абсолютный прирост ![]()
Темп роста:
![]() ¾ цепные темпы роста;
¾ цепные темпы роста;
![]() ¾ базисные темпы роста;
¾ базисные темпы роста;
![]() -- темп роста за весь период.
-- темп роста за весь период.
Темп прироста ![]() , )
, )
Абсолютное значение одного процента прироста ![]()
Средний уровень ![]() .
.
В общем виде средний уровень моментного ряда 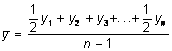 .
.
Средний абсолютный прирост 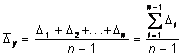
Средний абсолютный прирост ![]() .
.
Средний темп роста![]() ,
,
Средний темп роста ![]() ,
,
2.4. Характеристика параметров распределения показателя «наполняемость номерного фонда»
| данные | номер | сортируем X | |X-Xсреднее| | (X-Xреднее)^2 | (X-Xреднее)^3 | (X-Xреднее)^4 | число наблюдений на интервале |
| 65 | 1 | 37 | 32,2195122 | 1038,096966 | -33446,97786 | 1077645,311 | 6 |
| 51 | 2 | 38 | 31,2195122 | 974,6579417 | -30428,3455 | 949958,1033 | |
| 74 | 3 | 42 | 27,2195122 | 740,9018441 | -20166,98678 | 548935,5427 | |
| 89 | 4 | 45 | 24,2195122 | 586,584771 | -14206,79701 | 344081,6935 | |
| 88 | 5 | 46 | 23,2195122 | 539,1457466 | -12518,70124 | 290678,1361 | |
| 96 | 6 | 48 | 21,2195122 | 450,2676978 | -9554,460905 | 202740,9997 | |
| 37 | 7 | 51 | 18,2195122 | 331,9506246 | -6047,978454 | 110191,2172 | 6 |
| 66 | 8 | 54 | 15,2195122 | 231,6335515 | -3525,349661 | 53654,10216 | |
| 86 | 9 | 55 | 14,2195122 | 202,1945271 | -2875,107543 | 40882,62678 | |
| 54 | 10 | 58 | 11,2195122 | 125,8774539 | -1412,283629 | 15845,1334 | |
| 60 | 11 | 60 | 9,219512195 | 84,99940512 | -783,653052 | 7224,89887 | |
| 45 | 12 | 60 | 9,219512195 | 84,99940512 | -783,653052 | 7224,89887 | |
| 42 | 13 | 61 | 8,219512195 | 67,56038073 | -555,3133733 | 4564,405044 | 13 |
| 55 | 14 | 62 | 7,219512195 | 52,12135634 | -376,2907677 | 2716,635786 | |
| 58 | 15 | 62 | 7,219512195 | 52,12135634 | -376,2907677 | 2716,635786 | |
| 38 | 16 | 64 | 5,219512195 | 27,24330756 | -142,196776 | 742,1978065 | |
| 61 | 17 | 64 | 5,219512195 | 27,24330756 | -142,196776 | 742,1978065 | |
| 64 | 18 | 64 | 5,219512195 | 27,24330756 | -142,196776 | 742,1978065 | |
| 72 | 19 | 65 | 4,219512195 | 17,80428316 | -75,12538994 | 316,992499 | |
| 65 | 20 | 65 | 4,219512195 | 17,80428316 | -75,12538994 | 316,992499 | |
| 65 | 21 | 65 | 4,219512195 | 17,80428316 | -75,12538994 | 316,992499 | |
| 64 | 22 | 66 | 3,219512195 | 10,36525877 | -33,37107703 | 107,4385895 | |
| 90 | 23 | 67 | 2,219512195 | 4,926234384 | -10,93383729 | 24,26778521 | |
| 69 | 24 | 69 | 0,219512195 | 0,048185604 | -0,010577328 | 0,002321852 | |
| 67 | 25 | 69 | 0,219512195 | 0,048185604 | -0,010577328 | 0,002321852 | |
| 62 | 26 | 72 | 2,780487805 | 7,731112433 | 21,49626384 | 59,77009945 | 6 |
| 100 | 27 | 74 | 4,780487805 | 22,85306365 | 109,2487921 | 522,2625183 | |
| 83 | 28 | 78 | 8,780487805 | 77,09696609 | 676,9489706 | 5943,942181 | |
| 106 | 29 | 80 | 10,7804878 | 116,2189173 | 1252,896621 | 13506,83674 | |
| 60 | 30 | 81 | 11,7804878 | 138,7798929 | 1634,894836 | 19259,85868 | |
| 95 | 31 | 83 | 13,7804878 | 189,9018441 | 2616,940047 | 36062,71041 | |
| 46 | 32 | 84 | 14,7804878 | 218,4628198 | 3228,987043 | 47726,00361 | 5 |
| 78 | 33 | 86 | 16,7804878 | 281,584771 | 4725,129815 | 79289,98324 | |
| 84 | 34 | 88 | 18,7804878 | 352,7067222 | 6624,004295 | 124402,0319 | |
| 99 | 35 | 89 | 19,7804878 | 391,2676978 | 7739,465925 | 153090,4113 | |
| 69 | 36 | 90 | 20,7804878 | 431,8286734 | 8973,610482 | 186476,0032 | |
| 62 | 37 | 95 | 25,7804878 | 664,6335515 | 17134,57717 | 441737,7577 | 5 |
| 80 | 38 | 96 | 26,7804878 | 717,1945271 | 19206,81929 | 514367,9897 | |
| 64 | 39 | 99 | 29,7804878 | 886,8774539 | 26411,6432 | 786551,6182 | |
| 81 | 40 | 100 | 30,7804878 | 947,4384295 | 29162,61703 | 897639,5777 | |
| 48 | 41 | 106 | 36,7804878 | 1352,804283 | 49756,80144 | 1830079,429 | |
| сумма | 2838 | 586,9756098 | 12511,02439 | 41521,59905 | 8799085,808 | ||
| среднее | 69,2195122 | 14,31647829 | 305,1469363 | 1012,721928 | 214611,849 |
