Аксиоматика теории множеств

Рефераты >> Математика >> Аксиоматика теории множеств

X на W, получим, что существует некоторый класс Z1 такой, что

x1… xi-1xixj (Z1 φ (x1,…,xn, Y1,…, Ym)).

Далее, на основании

XZ v1…vmx1…xn (

ZX)

там же при Z1 = X, заключаем, что существует класс Z2 такой, что

x1 … xi xi+1 … xj ( Z2 φ (x1,…,xn, Y1,…, Ym)).

Наконец, применяя

XZ v1…vmx1…xn ( Z X)

(1)

там же при Z2 = Х, получаем, что существует класс Z такой, что

x1…xn ( Z φ (x1,…,xn, Y1,…, Ym)).

Для остающегося случая xi Yi теорема следует из (1) и

XZ x v1…vm ( Z x X).

2. Предположим, что теорема доказана для любого k < s и что φ со­держит s логических связок и кванторов.

(a) φ есть ψ. По индуктивному предположению, существует класс W такой, что

x1…xn ( W ψ (x1,…,xn, Y1,…, Ym)).

Теперь остается положить Z = .

(b) φ есть ψ θ. По индуктивному предположению, существуют классы Z1 и Z2 такие, что

x1…xn ( Z1 ψ (x1,…,xn, Y1,…, Ym)) и

x1…xn ( Z2 θ (x1,…,xn, Y1,…, Ym)).

Искомым классом Z в этом случае будет класс .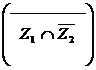

(c) φ есть x ψ. По индуктивному предположению, существует класс W такой, что

x1…xnx ( W ψ (x1,…, xn, x, Y1,…, Ym)).

Применим сперва

XZ x1 … xn ( Z y ( X)).