Рассмотрим 3 случая:

1. . Разделим на, причем . Тогда имеем уравнение: tg x = - 1. Следовательно, .

2. , cos x = -1. Следовательно, .

3. .

Получили ответ: .

Задача 21.

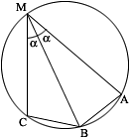
Решить задачу: В окружности проведены 3 хорды: МА = 6 см, МВ = 4 см, МС = 1 см. Хорда МВ делит вписанный угол АМС пополам. Найти радиус этой окружности.

Решение:

Отрезки и равны как хорды, стягивающие равные дуги, поэтому вычтем из первого уравнения второе и получим: . Значит, . Треугольник вписан в окружность, следовательно, радиус данной окружности можно найти с помощью теоремы синусов: . Ответ: .

Задача 22.

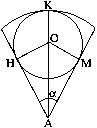
Решить задачу: В сектор радиуса с центральным углом вписан круг. Найти его радиус.

Решение:

Т.к. центры окружностей и точки касания лежат на одной прямой, то. Рассмотрим треугольник АОН (он прямоугольный, т.к. угол ): угол из равенства треуг-ков АОН и АОМ (т.к. ОН=ОМ=r, АН=АМ как отрезки касательных, проведенных из одной точки, сторона АО - общая).

Ответ: .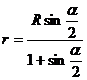

Задача 23.

Решить уравнение: .

Решение:

ОДЗ:.

Применяя формулы понижения степени, приведем это уравнение к более простому виду: , ,

.

Отсюда, используя формулу преобразования суммы косинусов в произведение, получаем: ,

,

.

Рассмотрим 2 случая:

1. ;

2. , следовательно, используя вновь формулу преобразования суммы косинусов в произведение, имеем:

a) ;

b) .

Таким образом, учитывая ОДЗ, получаем

Ответ: .

Задача 24.

Решить уравнение: .

Решение:

ОДЗ: .

Введем новую переменную, положив t = tg x. Так как , то уравнение примет вид: или . Число 2 является корнем полученного уравнения, поэтому это уравнение можно преобразовать следующим образом: . Квадратный трехчлен во второй скобке не имеет действительных корней. Следовательно, уравнение имеет только один корень. Найдем корни исходного уравнения:

.

Дополнительный случай рассматривать не надо, так как .

Ответ: .

Задача 25.

Решить уравнение: .

Решение:

ОДЗ: , т.е. .

Преобразуем уравнение следующим образом:

.

Рассмотрим 2 случая:

1. ; в этом случае исходное уравнение решений не имеет, т.к. данные значения не входят в ОДЗ;

2. ; эти значения входят в ОДЗ уравнения.

Ответ: .

Задача 26.

Решить систему:

Решение:

Каждое из уравнений этой системы является простейшим, поэтому нетрудно заметить, что