Анализ типичных ошибок при решении задач курса школьной математики: уравнения, тригонометрия, планиметрия

Рефераты >> Математика >> Анализ типичных ошибок при решении задач курса школьной математики: уравнения, тригонометрия, планиметрия

Т.к. первый до встречи в С со вторым прошел на 12 км меньше, то . Выразим теперь время, затраченное пешеходами от начала движения до их встречи: .

Т.к. первый вышел на 6 часов раньше, то: .

Сделаем замену: и решим уравнение: . Его корни: .

Получили 2 случая:

1. .

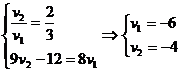2. .

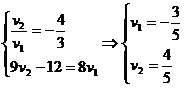Значит,

1. ;

2. .

Т.к. расстояние не может быть отрицательным, то подходит только второй случай.

Ответ: .

Задача 18.

Решить задачу: Две трубы, работая одновременно, наполняют бассейн за 12 часов. Одна первая труба наполняет бассейн на 10 часов медленнее, чем одна вторая. За сколько часов наполняет бассейн одна вторая труба?

Решение:

Положим объем бассейна = 1. Пусть (ч) – время наполнения бассейна одной второй трубой. Тогда одна первая труба наполнит бассейн за часов. Находим производительность этих труб: . За 12 часов совместной работы с общей производительностью заполняется весь бассейн: . Решаем полученное уравнение: .

Ответ: .

Задача 19.

Решить задачу: В ателье поступило по одному куску черной, зеленой и синей ткани. Хотя зеленой ткани было на 9 м меньше, чем черной, и на 6 м больше, чем синей, стоимость кусков была одинаковой. Сколько метров ткани было в каждом куске, если известно, что стоимость 4.5 м черной ткани = общей стоимости 3 м зеленой и 50 см синей?

Решение:

Пусть -количество черной, зеленой и синей ткани соответственно.

Известно: . Используем формулу:, где - цена ткани, S – стоимость куска, q – количество ткани.

Пусть S = 1. Получим - цены тканей. Составим уравнение, связывающее эти стоимости: .

Выразим и через : .

Подставляем в последнее уравнение: .

. Получили.

Ответ: .

Задача 20.

Решить уравнение: .

Решение:

По формулам приведения приведем все функции к одному аргументу: . Получили уравнение: . По формулам сокращенного умножения разложим на множители: . По основному тригонометрическому тождеству , поэтому остается решить уравнение: .

Рассмотрим 2 случая:

1. . Разделим на, причем . Тогда имеем уравнение: tg x = 1. Следовательно, .

2. . Разделим на, причем . Тогда имеем уравнение: tg x = -1. Следовательно, .

Получили ответ: .

Задача 21.

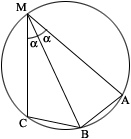
Решить задачу: В окружности проведены 3 хорды: МА = 6 см, МВ = 4 см, МС = 1 см. Хорда МВ делит вписанный угол АМС пополам. Найти радиус этой окружности.

Решение:

Отрезки и равны как хорды, стягивающие равные дуги, поэтому вычтем из первого уравнения второе и получим: . Значит, . Треугольник вписан в окружность, следовательно, радиус данной окружности можно найти с помощью теоремы синусов: . Ответ: .

Задача 22.

Решить задачу: В сектор радиуса с центральным углом вписан круг. Найти его радиус.