Анализ типичных ошибок при решении задач курса школьной математики: уравнения, тригонометрия, планиметрия

Рефераты >> Математика >> Анализ типичных ошибок при решении задач курса школьной математики: уравнения, тригонометрия, планиметрия

1. . Тогда уравнение примет вид: - корень исходного уравнения.

2. . Тогда уравнение примет вид: - корень исходного уравнения.

Ответ: .

Задача 12.

Решить уравнение: .

Решение:

ОДЗ: .

Оставляем корень в левой части уравнения, а все остальные слагаемые переносим в правую: . Затем возводим в квадрат: , причем т.к. , то для корректности возведения в квадрат необходимо, чтобы . Получим уравнение . Найдем его корни: . Оба корня удовлетворяют ОДЗ, но только один удовлетворяет дополнительному ограничению . Поэтому ответ: .

Задача 13.

Решить уравнение: .

Решение:

ОДЗ: .

Оставляем корень в левой части уравнения, а все остальные слагаемые переносим в правую: . Затем возводим в квадрат: . Получим уравнение . Его корни: . Оба корня удовлетворяют ОДЗ. Поэтому ответ: .

Задача 14.

Решить уравнение: .

Решение:

ОДЗ: .

Выделим полный квадрат под первым знаком корня: .

Получим уравнение: . Оставляем корень в левой части уравнения, а все остальные слагаемые переносим в правую и умножим уравнение на -1: . Возведем обе части уравнения в квадрат с учетом , получим . Найдем корни: . Учитывая ОДЗ и дополнительное ограничение , получаем ответ: .

Задача 15.

Решить систему уравнений: .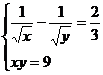

Решение:

ОДЗ: .

Из второго уравнения находим и подставляем в первое: .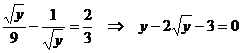

Делаем замену переменной: . Получаем квадратное уравнение относительно t: . Получим корни: .

Имеем 2 случая:

1. - это невозможно, т.к. - неотрицательная величина.

2. . Отсюда .

Ответ: (1; 9).

Задача 16.

Решить задачу: Два туриста идут навстречу друг другу из пунктов А и В. Первый выходит из А на 6 часов раньше, чем второй из В, и при встрече в пункте С оказывается, что он прошел на 12 км меньше второго. Продолжая после встречи путь с той же скоростью, первый приходит в В через 8 часов после встречи, а второй в А – через 9 часов. Определить расстояние АВ и скорость обоих пешеходов.

Решение:

Пусть (км/ч) – скорости первого и второго пешеходов, S(км)=АВ. Изобразим на чертеже движение пешеходов.

Из условия задачи имеем: .

Выразим теперь время, затраченное пешеходами от начала движения до их встречи: .

Т.к. первый вышел на 6 часов раньше, то: .

Сделаем замену: и решим уравнение: . Это уравнение корней не имеет. Следовательно, ответ: такая ситуация невозможна.

Задача 17.

Решить задачу: Два туриста идут навстречу друг другу из пунктов А и В. Первый выходит из А на 6 часов раньше, чем второй из В, и при встрече в пункте С оказывается, что он прошел на 12 км меньше второго. Продолжая после встречи путь с той же скоростью, первый приходит в В через 8 часов после встречи, а второй в А – через 9 часов. Определить расстояние АВ и скорость обоих пешеходов.

Решение:

Пусть (км/ч) – скорости первого и второго пешеходов, S(км)=АВ.