В курсе алгебры использовали теорему Лапласа об алгебраических дополнениях: для любых фиксированных натуральных чисел <, определитель квадратной матрицы над кольцом равен сумме произведений всех её миноров порядка , содержащихся в строках с номерами на их алгебраические дополнения, то есть

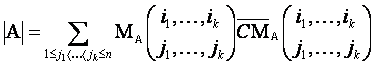. (1)

1.Рассмотрим сначала случай, когда . Обозначим в этом случае правую часть равенства (1) через и будем вычислять её, пользуясь определениями миноров и их алгебраических дополнений:

.

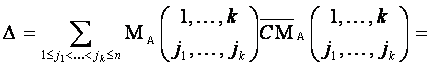
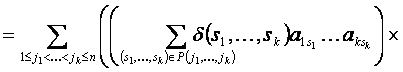
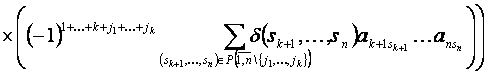Перемножая в скобках 1-ую сумму на 2-ую почленно и пользуясь свойствами операций в кольце , получим

. (2)

Запишем полученную сумму сумм в виде одной суммы. Заметим, что число слагаемых во внутренней сумме равно , а во внешней - . Значит общее число слагаемых в сумме будет равно , то есть числу всех перестановок из . Заметим теперь, что наборы индексов , соответствующие слагаемым суммы (2), являются перестановками множества и любая перестановка из может быть представлена в виде такого набора индексов при подходящем выборе множества и перестановок

.

Следовательно, в результате суммирование будет производиться по всем перестановкам из . Отсюда, с учётом утверждения 1, получим

,

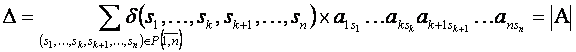и равенство (1) в рассматриваемом случае доказано.

2. Пусть теперь - любые числа из множества , удовлетворяющие условию . Сведём этот случай к первому. Для этого осуществим в матрице следующую перестановку строк. Переставляя -ую строку поочерёдно со всеми предыдущими, поставим её на первое место, затем -ую строку таким же образом поставим на второе место, и т.д., и, наконец, поставим -ую строку на -ое место. В итоге получим некоторую матрицу . Так как для перехода от мы произвели перестановок строк, то по свойствам определителей:

. (3)

По доказанному в случае 1 имеем:

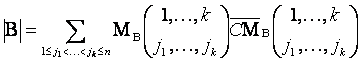. (4)

Непосредственно из построения матрицы следует, что

.

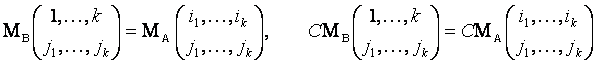Из последнего равенства, используя определение алгебраического дополнения, получим:

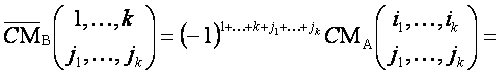
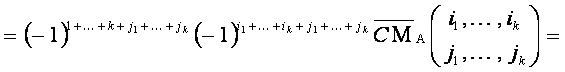
Из найденных соотношений между минорами и алгебраическими дополнениями матриц А, В и равенств (3), (4) легко следует равенство (1).

В 1785 г., в возрасте 36 лет, Лаплас стал действительным членом академии. Этот же год, знаменующий такой почет в научной дея­тельности, выделяется как веха еще большего значения в общест­венном положении Лапласа — в этом году он экзаменовал одного из 16 кандидатов в Военную школу. Этому юноше предстояло играть важную роль в последующем отходе Лапласа от математики и по­гружении в мутные воды политики. Имя юноши было Наполеон Бо­напарт (1769—1821).

Лаплас прошел через революционные годы сравнительно спо­койно. Но все же ни один человек с его известностью и беспокойным честолюбием не мог в то время избежать опасности полностью. Лап­лас и Лагранж не питались лебедой, как многие другие менее нуж­ные ученые, и не были столь беспечны, чтобы выдать себя, как это случилось с их несчастным другом Кондорсе: его не то отравили в тюрьме, не то не препятствовали ему покончить с собой.

После революции Лаплас активно занялся политикой, возмож­но надеясь побить в этом рекорд Ньютона. Французы вежливо говорят о «разносторонности» Лапласа в политике. Это выражение чересчур мягко. Пресловутые недостатки Лапласа как политика были не чем иным, как блестящими способностями в азартной игре. Лаплас всегда получал лучшие посты при каждом падении прави­тельства. Ему ничего не стоило за ночь переметнуться от неистовых республиканцев к ревностным монархистам.

Наполеон подсовывал Лапласу все, включая портфель министра внутренних дел (об этом скажем позже). Все наполеоновские орде­на украшали грудь гибкого математика, включая Большой Крест Почетного легиона. Он был пожалован также титулом графа им­перии. Как же он поступил, когда Наполеон пал? Подписался под декретом об изгнании своего благодетеля.