Известно, что А*А — самосопряженный положитель­ный вполне непрерывный оператор из F в F. Пусть l1>=l2>=…>=ln>=… — полная система его собственных значений, a j1, j2,…, jn,…—отвечающая им полная ортонормированная система его собственных элементов (функций, векторов). Элемент А*и можно представить в виде ряда

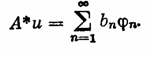(2;2,2)

В этих условиях справедлива

Теорема 3. Квазирешение уравнения (2, 0,1) на множестве SR выражается формулами:

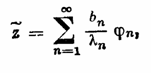(2;2,3)

если

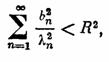(2;2,4)

и

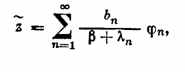
если

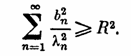(2;2,5)

Здесь b — корень уравнения

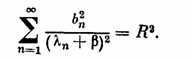(2;2,6)

Доказательство. Квазирсшение минимизирует функционал

rU2 (Az, u) == (Az — u, Az — u) (2;2,7)

(где (v,w ) — скалярное произведение элементов v и w из U), уравнение Эйлера для которого имеет вид

A*Az=A*u. (2;2,8)

Решение этого уравнения будем искать в виде ряда по системе {jn}:

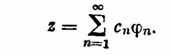(2;2,9)

Подставляя этот ряд в уравнение (2; 2,8) и используя разложение (2;2,2), находим сn=bn/ln. Следователь­но, неравенство (2; 2,4) означает, что ||z||<R и речь идет о нахождении безусловного экстремума функциона­ла (2; 2,7). Ряд (2; 2,3) и будет решением задачи.

Если же выполняется неравенство (2; 2,5), то это означает, что ||z||>=R и надо решать задачу на услов­ные экстремум функционала (2; 2,7) при условии, что || z ||2 = R2. Методом неопределенных множителей Лагранжа эта задача сводится к нахождению безусловного экстремума функционала

(Аz-u, Аz-u) + b (z, z),

а последняя — к решению отвечающего ему уравнения Эйлера A*Az+bz=А*и. Подставляя сюда z в виде ряда (2; 2,9) и используя разложение (2; 2,2), находим

Параметр b определяем из условия || z ||2 = R2 , которое эквивалентно (2; 2,6).

2.3. Приближенное нахождение квазирешений

В предыдущем параграфемы видели, что нахождение квазирешения связано с нахождением элемента в беско­нечномерном пространстве. Для приближенного нахожде­ния квазирешения естественно переходить к конечномер­ному пространству. Можно указать достаточно общий под­ход к приближенному нахождению квазирешений урав­нения (2; 0,1) , в котором А—вполне непре­рывный оператор.

Будем полагать, что выполнены указанные в 2.2. дос­таточные условия существования единственного квазире­шения на заданном множестве М, т. е. полагаем, что множество М — выпуклый компакт и сфера в пространст­ве U строго выпукла. Пусть

M1 Ì M2 Ì .Ì Mn Ì .

— возрастающая цепочка компактных замкнутых множеств Мn такая, что замыкание их объединения совпадает с М. Квазирешение уравнения (2; 0,1) сущест­вует на каждом множестве Мn . Но оно может быть не единственным. Обозначим через Тn совокупность всех квазирешений на множестве Мn .

Покажем, что в качестве приближения к квазиреше­нию z1 на множестве М можно брать любой элемент z1n из Тn . При этом

Пусть Nn = АМn и Вn — множество проекций элемен­та и на множество Nn . Очевидно, что Вn = АТn и N1 Í N2 Í …Í Nn; тогда

r U(u,N1)>= …>=r U (u,Nn)>=… r U (u,N)= r U (u,Az1) . (2;3,1)

Так как множество всюду плотно на N, то для всякого e >0 найдется такое число n0(e), что для всех п >n0(e)

rU(u,Nn)< rU(u,N)+ e (2; 3,2)

Из (2; 3,1) и (2; 3,2) следует, что

(2;3,3)

(2;3,4)

Каждое множество Вn есть компакт, так как оно является замкнутым подмножеством компакта Nn. Поэтомув Вnнайдется такой элемент уn , что

rU(yn ,u) = inf rU(y,u)

yÎBn

Последовательность {yn} имеет хотя бы одну пре­дельную точку, принадлежащую N, так как N — компакт. Пусть у0 — какая-нибудь предельная точка множества {yn} и {уnk} — подпоследовательность, сходящаяся к y0 , т. е.

Из (2; 3,3) и (2; 3,4) следует, что

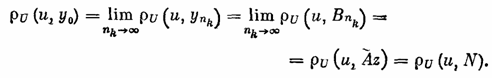
Таким образом,

rU(u,y0)= rU(u,N).

Отсюда и из единственности квазирешения на множестве М следует, что

y0=Az1.

Так как у0 — произвольная предельная точка множества {yn}, то последовательность {уn} сходится к Аz1. Это и означает, что в качестве приближения к квазирешению мож­но брать любой элемент z1n из множества Тп , так как в силу леммы параграфа 2.1. z1nàz* при nà¥.

Если в качестве Мп брать конечномерные (n-мерные) множества, то задача нахождения приближенного квази­решения на компакте М сводится к минимизации функ­ционала rU(Az, u) на множестве Мп , т. е. к нахождению минимума функции п переменных.

2.4. Замена уравнения Аz=u близким ему

Уравнения вида (2; 0,1), в которых правая часть u не принадлежит множеству N=AM, изучались М. М. Лав­рентьевым . Ему принадлежит идея замены исходного уравнения (2; 0,1) близким ему, в некотором смысле, уравнением, для которого задача нахождения решения устойчива к малым изменениям правой части и разрешима для любой правой части u ÎU. В простей­шем случае это делается следующим образом.

Пусть F ºU ºН — гильбертовы пространства, А — линейный, ограниченный, положительный и самосопря­женный оператор, SR º {х, ||x||<=R, xÎF} есть шар радиуса R в пространстве F, В — вполне непрерывный оператор, определенный на SR при любом R > 0. В ка­честве класса корректности М берется множество DR=BSR — образ шара SR при отображении с помощью оператора В. Предполагается, что искомое точное решение zT уравнения (2; 0,1) с правой частью u=uT существует и принадлежит множеству DR. Уравнение (2; 0,1) заме­няется уравнением

(A+aE)z º Az+az=u , (2:4,1)