которая называется приведённой длиной физического маятника.

Мы доказали это утверждение только для малых колебаний маятников. Но оно справедливо и для колебаний с конечными амплитудами, когда колебания не изохронны. Требуется только, чтобы угловые амплитуды физического и математического маятников были одинаковы. Доказательство этого приводим ниже.

I. Отложим от точки подвеса А вдоль прямой АС отрезок АА´, длина которого равна приведённой длине физического маятника l (на рис. выше). Точка А´ называется центром качания. Центр качания можно определить как математическую точку, в которой надо сосредоточить всю массу физического маятника, чтобы период его колебаний остался без изменений. По теореме Гюйгенса-Штейнера

I=Ic+ma2,

где Ic – момент инерции маятника относительно параллельной оси, проходящей через центр масс С. Подставив это выражение в формулу (1), получим:

l=a+Ic/ma (2)

Отсюда следует:

1. l›a, т. е. точка подвеса А и центр качания А´ лежат по разные стороны от центра масс С;

2. всем точкам подвеса, одинаково удалённым от центра масс маятника, соответствует одна и та же приведённая длина l, а следовательно, один и тот же период колебаний Т.

Точка подвеса и центр качания являются взаимными или сопряжёнными точками в следующем смысле. Если маятник подвесить за центр качания А´, то его период не изменится и прежняя точка подвеса А сделается новым центром качания.

Это положение называется теоремой Гюйгенса. Для её доказательства обозначим а´ длину отрезка А´С и допустим, что маятник подвешен за точку А´. Тогда его приведённая длина:

l´=a´+Ic/ma´. (3)

Но a´=l-a, или в силу соотношения (2)

a´=Icma.

Подставив это значение в формулу (3), получим

l´=Ic/ma+a.

Таким образом, l´=l, т. е. приведённая длина, а с ней и период колебаний физического маятника остались без изменений. Это и доказывает теорему Гюйгенса.

II. Следующее доказательство теоремы Гюйгенса глубже раскрывает её содержание.

Перемещая точку подвеса маятника вдоль одной и той же прямой, проходящей через центр масс С, посмотрим, как будет меняться его период колебаний. Когда точка подвеса А бесконечно удалена от С, маятник ведёт себя как математический. Его период колебаний бесконечно велик. При приближении точки подвеса А к центру масс С период колебаний сначала убывает. Когда точка подвеса совместиться с С, маятник при любом отклонении будет в безразличном равновесии. Это значит, что его период колебаний становится бесконечно большим. Поэтому по мере приближения точки А к С убывание периода должно смениться возрастанием. Положению точки подвеса, где это происходит, соответствует минимальный период колебаний. Когда точка подвеса переходит через точку Сна другую сторону прямой АА´, период колебаний, перейдя через бесконечность, начинает уменьшаться. При этом двум положениям точки подвеса, находящимся по разные стороны от С на одинаковых расстояниях, соответствуют равные периоды колебаний.

Вместо периода колебаний можно пользоваться приведённой длиной маятника l, однозначно определяющей его период колебаний. При удалении точки подвеса в бесконечность или при приближении её к центру масс С приведённая длина l стремится к бесконечности и достигает минимума в каком-то промежуточном положении. Графически это представлено на рис. 2:

На оси абсцисс отложена величина а, на оси ординат – приведённая длина маятника l. Кривая состоит из двух ветвей, симметрично расположенных относительно оси ординат. Одна ветвь соответствует случаю, когда точка подвеса расположена по одну, а вторая – по другую сторону от центра масс С. Аналитически кривая изображается уравнением (3), которое можно представить в виде:

a2-la+Ic/m=0 (4)

Фиксированному значению приведённой длины l0 соответствует на рис. Горизонтальная прямая l=l0. Точки пересечения её с кривой определяют положение точек подвеса физического маятника, при которых его приведённая длина равна заданному значению l0. Таких точек пересечения четыре. Две из них расположены по одну, две остальные – по другую сторону от центра масс С. Их положение легко найти из квадратного уравнения:

a2-l0a+Ic/m=0 (5)

Если l0›2·(Ic/m)½, это уравнение имеет два вещественных положительных корня a1 и а2, причём

a1+a2=l0 (6)

В этом случае по одну и ту же сторону от центра масс С имеются две точки подвеса А1 и А2 (рис. 3), которым соответствует одна и та же приведённая длина l0. По другую сторону от центра масс С лежит вторая пара симметрично расположенных точек подвеса А1´ и А2´, характеризующаяся той же приведённой длиной l0. Если l0=2(Ic/m)½, то корни уравнения (5) совпадают, т. е. обе точки подвеса по каждую сторону от центра масс сливаются в одну.

Если l0<2(Ic/m)½ , то корни уравнения (5) мнимые. Таких точек подвеса не существует.

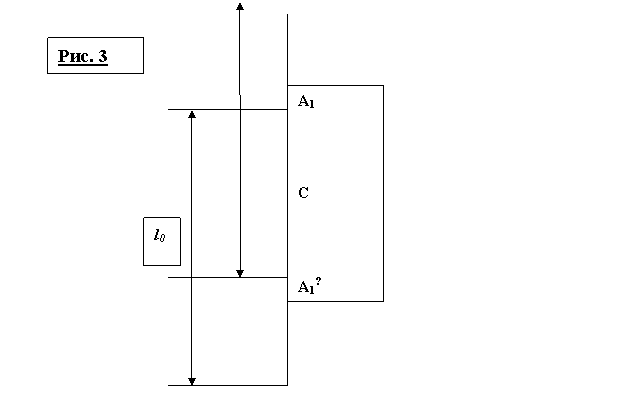
Из соотношения a1+a2=l0 следует, что расстояние между точками А1 и А2´ , а также между точками А1´ и А2 равно приведённой длине маятника l. Если одну из точек каждой пары принять за точку подвеса, то вторая будет центром качания.