Постановка задачи

Пусть имеются две диэлектрические среды 1 и 2 , с электрической и магнитной проницаемостью и соответственно. Из среды 1 в 2 падает плоская монохроматическая волна (границу раздела будем считать плоской).При переходе через границу раздела волна разделится на две части : отраженную волну (в среде 1) и преломленную волну (в среде 2) , необходимо выяснить соотношения между углами и , а также между интенсивностями падающей и отраженной волн (рис 1).

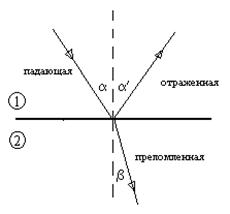
рис.1

Данная волна должна представлять собой точное решение уравнений Максвелла : и (1) (учитывая , что среда диэлектрическая , т.е. )

для плоской монохроматической волны точное решение этих уравнений будет (если оси Х направить в сторону распространения волны):

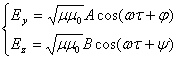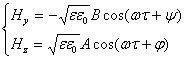и (==0) (2)

где A и B , и , - постоянные (не зависят от времени и координаты) ,

и - характеристики среды , в которой распространяется волна ,

, t - рассматриваемый момент времени

x - рассматриваемая координата на оси Х

V - скорость распространения волны в данной среде

(естественно , в силу линейности уравнений Максвелла любая сумма таких волн будет также их точным решением )

Также она должна удовлетворять условиям на границе раздела : и не терпят разрыва на поверхности раздела , и также не терпят разрыва , поскольку на границе раздела не течет ток и нет поверхностной плотности заряда:

(3)

(индексом 1 обозначаем все , относящееся к первой среде , индексом 2 - ко второй)

Таким образом , необходимо построить точное решение уравнений (1) , удовлетворяющих условиям (3). Для этого рассмотрим два случая : случай ТМ -волны (р-волны ) - вектор перпендикулярен плоскости падения (трансверсальная магнитная) , и случай ТЕ-волны (s-волны)- вектор перпендикулярен плоскости падения (трансверсальная электрическая). Любая плоская волна (с любой поляризацией) может быть представлена как линейная комбинация двух таких волн.

Случай ТМ -волны (p - волны)

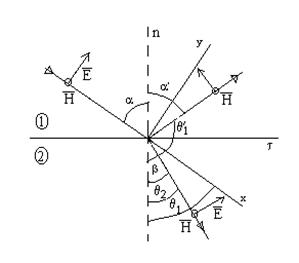
рис.2

Из рисунка видео , что , запишем условия равенства на границе раздела :

( учитывая , что волна в среде 1 есть сумма падающей и отраженной волн)

подставляем значения:

подставляем из (2) :

Аналогично , поскольку получаем для вектора на границе раздела:

( c учетом (2) )

для выполнения равенств для и потребуем равенства аргументов косинусов :

потребуем также равенства начальных фаз:

из рисунка видно , что : , (4)

(,и - соответственно : угол падения , угол отражения и угол преломления ) , тогда имеем :

из равенства аргументов получаем :

(т.к. , )

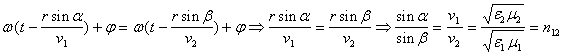т.е. получены , как и следовало ожидать , законы отражения и преломления света

разделим теперь выражения дляи на , получим (c учетом (4) ) следующую систему :

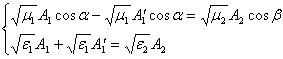(5)

здесь неизвестными являются и , а - заданно.

Умножим первое уравнение на а второе на и вычтем из первого второе , тогда члены с сократятся и получим: