Вывод и анализ формул Френеля на основе электромагнитной теории Максвелла
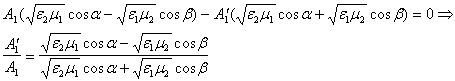
поскольку для неферромагнетиков магнитная проницаемость
незначительно отличается от единицы , то для сравнительно широкого класса сред можно считать 
, тогда:
.
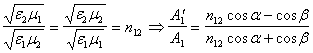( разделим числитель и знаменатель на 
, и учтя , что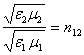
)
применив закон преломления , получим (6):
из второго уравнения системы (5) получаем для 
:
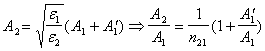(поскольку полагаем ,) , тогда:
(7)
проверим теперь выполнение еще двух условий на границе раздела ,которые мы не учли -
и 
. Второе равенство выполняется заведомо , поскольку 
, проверим первое равенство 
:
из рисунка видно , что 
, а 
подставим значения 
,
и 
( из 2) , сократив сразу на 
, и учитывая (4) :
(выражая через второе уравнение системы (5) )
Таким образом действительно получено точное решение уравнений (2) , удовлетворяющее всем начальным условия. Итак , имеем следующие формулы Френеля для случая s-волны для отражения и преломления (из (6) и (7) ):
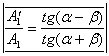и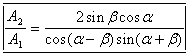 
Случай ТЕ -волны ( s - волны)
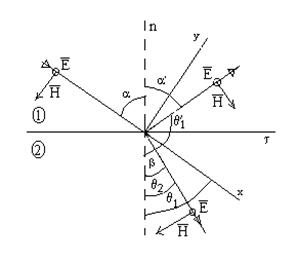
рис.3
Из рисунка видно , что 
Условия (3) для 
и 
:
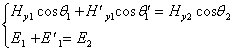
подставляя значения 
и 
из (2) получим :
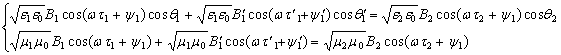как и в случае ТМ-волны предполагаем равенство аргументов косинусов и совершенно аналогично получаем в этом случае закон отражения и преломления света , сокращая на 
и с учетом (4) получим систему :
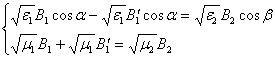(8)
умножим первое уравнение на 
а второе на 
и вычтем из первого второе :
поскольку мы полагаем 
(см. выше) то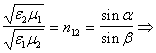 
(9)
из второго уравнения системы (8) получаем:
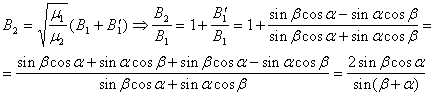(10)
проверим теперь неучтенные условия на границе раздела : и .
Второе условие выполняется , поскольку 
, проверим выполнение равенства : 
из рисунка видно , что 
, а 
подставим значения 
,
и 
( из 2) , сократив сразу на 
, и учитывая (4) получим : 
подставляем 
из второго уравнения системы (8) :
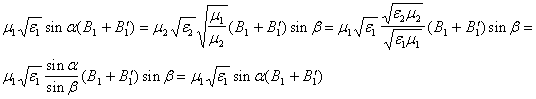
таким образом мы действительно нашли точное решение уравнений (2) , удовлетворяющее всем начальным условиям . В случае p-волны имеем следующие формулы Френеля для отражения и преломления (из (9) и (10))
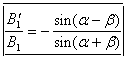и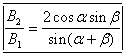 
Анализ формул Френеля
Исследуем отношения энергий (точнее плотности потока энергий ) падающей и отраженной ТМ и ТЕ волн и падающей и прошедшей волн в зависимости от угла падения 
. Для этого рассмотрим отношение нормальной составляющей вектора Пойтинга 
падающей и отраженной (
и 
в случае ТМ и ТЕ волн соответственно) и падающей и прошедшей (
и 
) волн. Тогда с из полученных формул Френеля для отражения и преломления , с учетом (2) будем иметь:
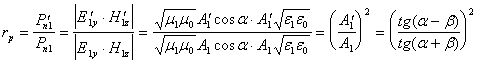
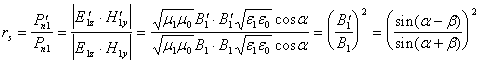
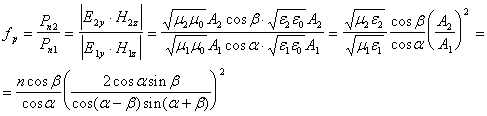
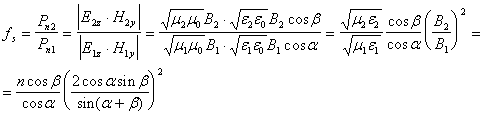
А. Отражение
