Вывод и анализ формул Френеля на основе электромагнитной теории Максвелла
Итак , в обоих случаях 
сначала монотонно убывает от 
при 
до 0 при 
, а затем монотонно возрастает до 1 при 
или 
.
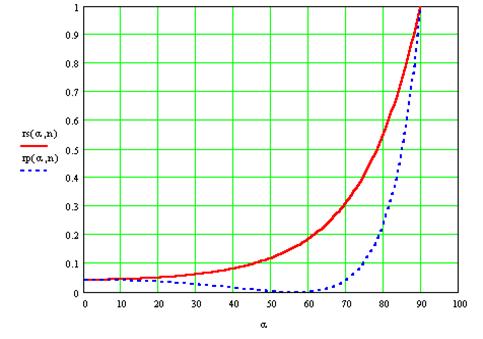
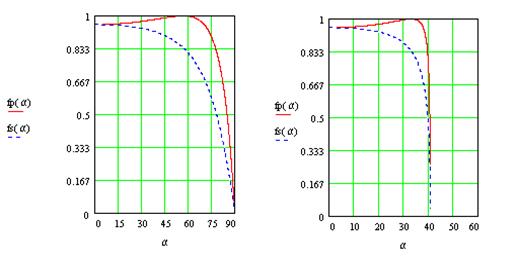
Полученные зависимости иллюстрируются следующими графиками :
на первом показана зависимость (сплошная линия) и 
(пунктирная линия) от 
для случая падения волны из воздуха в стекло (n=1.51)
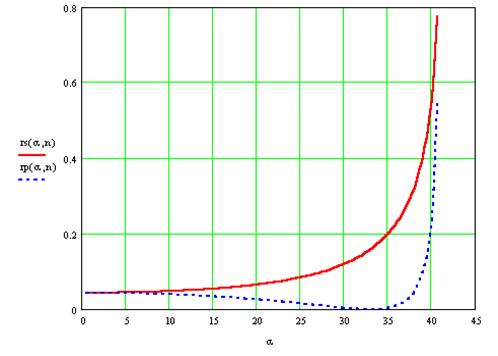
на втором -для случая падения волны из стекла в воздух
В. Преломление
Для анализа поведения 
и 
воспользуемся следующим соображением - падающая волна на границе раздела разделяется на две - прошедшую и отраженную , причем энергия падающей волны (энергия , переносимая волной через границу раздела сред) уходит в энергию отраженной и преломленной волн (поскольку никаких других источников нет). Поэтому , поскольку коэффициент 
показывает отношение энергии прошедшей волны к энергии падающей , - отношение энергии отраженной волны к энергии падающей в p-волне , а 
и - аналогичные отношения в s-волне , должны выполнятся соотношения :
и 
Действительно , проверим это :
рассмотрим отдельно числитель:
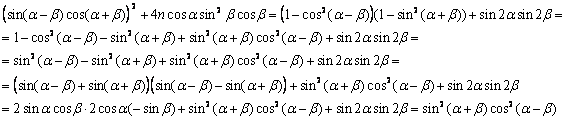таким образом действительно , аналогично
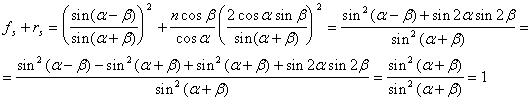
Таким образом , используя предыдущее исследование , можно сказать , что :
Для случая падения из воздуха в стекло (а можно заметить , что если среды поменять местами , то это значение не изменится ) 
Между этими точками и ведут себя противоположно и .
Окончательно , монотонно возрастает от 
( )до 
, а затем монотонно убывает до 0 ( при 
) , монотонно убывает от до 0 (при тех же пределах изменения). Причем как для случая падения из менее оптически плотной среды , так и из более оптически плотной. Ниже на рисунке представлены графически зависимости для обоих этих случаев.
С. Набег фаз при отражении и преломлении
Из формул Френеля следует , что отношения 
,
,
и 
могут в принципе получится и отрицательными . Поскольку амплитуда есть существенно положительная величина , в этом случае имеет место сдвиг фазы волны на
. Далее выясним , когда такой сдвиг имеет место.
В случае отраженной p-волны 
, как установлено в п. А , эта функция
при n>1 больше 0 при 
и меньше 0 при 
, при n<0 промежутки знакопостоянства меняются местами . Таким образом , в случае падения из менее оптически плотной среды в более плотную сдвиг фаз на в отраженной p-волне наблюдается при , а в случае падения из более плотной в менее плотную - при.
В случае отраженной s-волны 
, эта функция меньше 0 при 
и больше 0 в противном случае. Таким образом , сдвиг фаз на в отраженной s-волне наблюдается при падении из менее оптически плотной среды в более плотную , и не наблюдается при падении из более плотной среды в менее плотную.
В случае произвольно падающей линейно поляризованной волны , которая представляется в виде суммы p и s-волн , в отраженной волне , таким образом , можно получить , в общем случае волну произвольной (эллиптической) поляризации .
Для исследования сдвига фаз в прошедшей волне , воспользуемся соотношениями , возникшими как промежуточные результаты при выводе (7) и (10) :
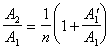и 
из этих соотношений видно , что , поскольку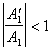 
и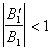 
, то всегда 
и 
. То есть , в прошедшей волне изменения фазы не происходит (причем это верно для волн произвольной поляризации).
