Вывод и анализ формул Френеля на основе электромагнитной теории Максвелла
Исследуем сначала поведение 
и 
на границах отрезка 
:
при 
(просто положить 
равным нулю нельзя , потому что будет неопределенность ):
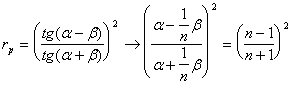
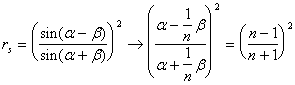
для случая падения из воздуха в стекло (
) : 
т.е. это величина порядка нескольких процентов (можно заметить , что если поменять среды местами - т.е. рассматривать падение из воды в воздух , то это значение не изменится)
В случае падения из оптически менее плотной среды в оптически более плотную при
:
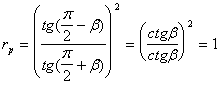
Действительно, преломленной волны при скользящем падении не образуется и интенсивность падающей волны не меняется.
В случае падения из оптически более плотной среды в оптически менее плотную , необходимо учесть явление полного внутреннего отражения , когда прошедшей волны нет - вся волна отражается от поверхности раздела. Это происходит при значениях больших , чем 
, вычисляемого следующим образом:
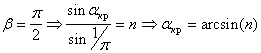[1][к1]
Для падения из стекла в воздух 
Здесь не рассматривается полное внутреннее отражение , поэтому в случае падения из оптически более плотной среды в оптически менее плотную изменяется до , в этом случае:
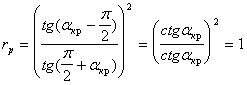
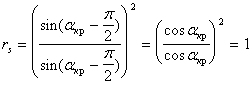
Далее исследуем поведение этих функций между крайними точками , для этого исследуем на монотонность функции: 
и 
Нам понадобится производная 
, найдем ее как производную функции , заданной неявно :
Знак этой производной ( поскольку 
, 
) зависит только от знака выражения 
, это выражение > 0 , когда 
(то есть падение из оптически мене плотной среды в оптически более плотную ) и <0 , когда 
(из более оптически плотной в менее оптически плотную ) , следовательно в первом случае монотонно возрастает, а во втором , убывает . Но в случае 
, следовательно по модулю это выражение будет возрастать , в случае
оно также будет по модулю возрастать . Таким образом , 
, как квадрат этого выражения , в обоих случаях монотонно возрастает от 
при 
до 1 при 
.или
.
Знак этой производной ,( поскольку ,
есть >0 при и <0 при .
Знак функции меняется следующим образом :
при если невелико
>0 , но эта функция проходит через нуль. Поскольку числитель , при рассматриваемых пределах изменения в 0 обращаться не может[2][к2] это происходит тогда , когда знаменатель обращается в бесконечность т.е.:
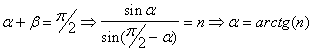
Это есть угол Брюстера (
) , при котором 
обращается в 0 , то есть отраженная волна отсутствует . Для случая падения из воздуха в стекло 
, для обратного случая (из стекла в воздух) 
При переходе через этот угол меняет знак на минус , следовательно как квадрат этой функции сначала убывает (до нуля) , а затем возрастает (до 1).
При для небольших<0 , при переходе через знак будет меняться на плюс. Переход через действительно будет иметь место , хотя изменяется до ,а не до 
, поскольку 
. Таким образом снова монотонно убывает до 0 , а затем монотонно возрастает до 1.
