В цепи главной отрицательной обратной связи системы автоматического регулирования устанавливаются, как правило, безынерционные, апериодические или интегродифференцирующие звенья. Идеальные (или реальные) интегрирующие и дифференцирующие звенья в главной обратной связи не устанавливают, так как наличие в цепи интегрирующего звена приводит к нулевому уровню выходной функции, а дифференцирующих – к прекращению прохождения сигнала по цепи обратной связи в установившемся режиме вследствие большого сопротивления:

Заметим, что не во всех случаях целесообразно предъявлять к системе такие жёсткие требования, как

Например, в технической литературе показано, что целесообразно применение апериодических обратных связей для улучшения динамических свойств автоматических систем управления судовыми механизмами и курсом судов. Один из способов определения эталонной передаточной функции – преобразование исходной структурной схемы к эквивалентной с единичной обратной связью (рис. 1).

На рис.1 обозначено:

u(t) – входное воздействие;

Wпк(p) – передаточная функция прямого канала САУ;

Wос(p) – передаточная функция обратной связи;

y(t) – выходная функция;

ФэтI(р) - эталонная передаточная функция контура с единичной обратной связью;

Wэт(р) - эталонная передаточная функция последовательно с контуром включенного звена эквивалентной структурной схемы.

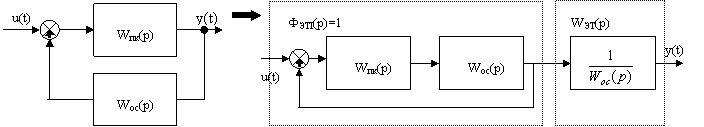
Рис.1. Преобразование типовой структурной схемы непрерывной САУ.

Если Wос(р)=1, тогда Wэт(р)=1 и Фэт(р)=ФэтI(p)Wэт(р)=1, т.е. y=u.

Если Wос(р) - интегродифференцирующая цепь, апериодическое или безынерционное звено и допускается лишь изменение масштаба копирования, то т.е. y=kЭТu.

В интегрирующих системах 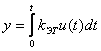и

Переходная функция САУ

Переходной функцией называется реакция системы (звена) на единичное ступенчатое воздействие при нулевых начальных условиях.

Если u(t)=1(t), то

Импульсной переходной функцией (весовой функцией) называется реакция системы (звена) на воздействие вида d - функции (единичный мгновенный импульс) при нулевых начальных условиях.

Если u(t)= d(t), тогда y(t)=k(t).

В преобразованиях Лапласа

Частотные характеристики

Частотными называются характеристики звеньев (систем) в форме графиков или таблиц, отображающие изменение амплитуды и фазы выходной функции (т.е. реакцию) звеньев или систем относительно синусоидального входного воздействия в установившемся режиме при изменении частоты от 0 до ¥. Очевидно, что при экспериментальном определении частотных характеристик диапазон изменения частоты входного гармонического воздействия ограничен техническими возможностями аппаратуры. Для линейных систем справедлив ПРИНЦИП СУПЕРПОЗИЦИИ, который можно сформулировать следующим образом.

Это позволяет ограничиться изучением систем только с одним входом.

В качестве входных воздействий были выбраны гармонические воздействия в виду нескольких обстоятельств:

1) реально встречающиеся воздействия, как правило, могут быть представлены в виде суммы гармоник различных частот (разложение Фурье);

2) в установившихся режимах гармонические сигналы передаются линейными элементами и системами без искажений;

3) обычно не возникает затруднений в экспериментальном исследовании поведения таких элементов и систем при гармонических воздействиях.

Пусть на вход стационарного линейного элемента или системы воздействует гармонический сигнал u=Um×coswt. (1)

Решим уравнение линейной стационарной системы с одним входом

(2)

здесь p – оператор дифференцирования, подставив в правую часть выражение (1). Общее решение имеет вид где yс – общее решение однородного уравнения, а yв – частное решение неоднородного уравнения.

Составляющая yс(t) определяет свободные движения (переходный процесс). В устойчивых системах она со временем затухает: при Вынужденное движение описывается частным решением yв(t). Чтобы найти его, отобразим входное воздействие (1) с помощью формулы Эйлера в пространство Фурье где , . (5)

Используя принцип суперпозиции, решение уравнения (2) можно также представить в виде суммы y=y1+y2, где y1 – решение при u=u1, а y2 – решение при u=u2. Найдем отдельно каждое из этих решений. Подставим выражение для u1 в правую часть уравнения (2) вместо u. Так как

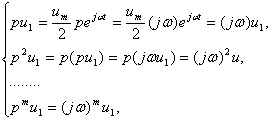
уравнение (2) примет вид

(3)

Частное решение последнего уравнения будем искать в виде

(4)

где A1 не зависит от времени. При подстановке этого выражения в (3) получим

,

откуда

Очевидно, это выражение совпадает с частотной передаточной функцией рассматриваемой системы:

Подставив это выражение в формулу (4), получим

(6)

Теперь найдем частное решение y2 исходного уравнения, подставив вместо u выражение для u2 из (5). Так как

то (2) в этом случае

Частное решение этого уравнения будем искать в виде