Анализ тенденций развития рынка товаров и услуг

Рефераты >> Статистика >> Анализ тенденций развития рынка товаров и услуг

Тогда

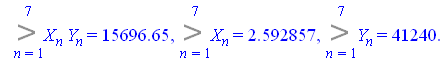
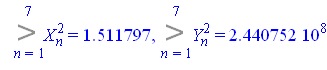
Откуда

Смысл коэффициента beta заключается в том, что при изменении значения X на 1 единицу Y меняется на 763,58 единиц. Тогда гиперболическая регрессия будет иметь вид

Нарисуем точки и регрессию:

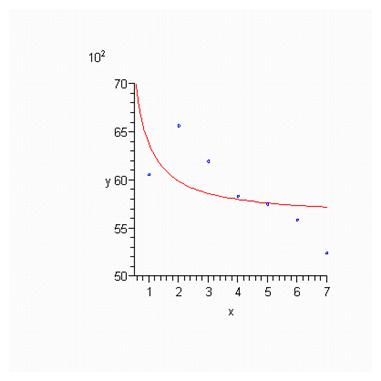
Дисперсионный анализ

Среднее Y

Остаточная вариация (RSS)

Общая вариация (TSS)

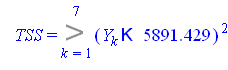
Объясняемая вариация (ESS)

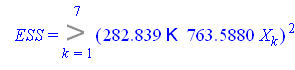
Правило сложения дисперсий выполняется

Подсчитаем оценку дисперсии ошибки, т.е.

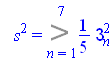
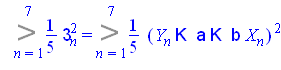
Среднее X

Найдем оценки дисперсий коэффициентов регрессии

Получим

Эластичность

Подсчитаем функцию эластичности по формуле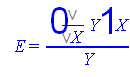

В нашем случае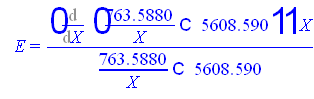

или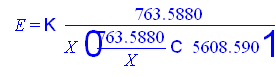

Значение эластичности в средней точке

Показывает, что при изменении X на 1% Y меняется на -0,268 процентов.

Изучение качества регрессии

Доверительные интервалы для оцененных параметров

уровень доверия

Количество степеней свободы =5. Критическое значение статистики Стьюдента

Доверительный интервал для beta

равен

Можем на данном уровне значимости принять гипотезу beta=0 т.к. попадает в доверительный интервал.

Доверительный интервал для alpha

равен

Мы НЕ можем на данном уровне значимости принять гипотезу alpha=0 т.к. НЕ попадает в доверительный интервал.

Критерий Фишера значимости всей регрессии

Коэффициент корреляции

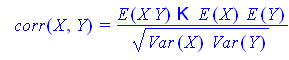
показывает, что связь СРЕДНЕЙ силы

Коэффициент детерминации

показывает, что регрессия объясняет 28, 89 процентов вариации признака.

Убедимся в значимости модели с помощью статистики Фишера

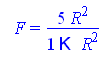
которая Меньше критического значения

Следовательно, регрессия НЕЗНАЧИМА

Проверим значимость коэффициента корреляции

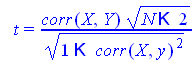
поэтому выборочный коэффициент корреляции НЕЗНАЧИМО отличается от нуля. Средняя ошибка аппроксимации

Колеблемость признака

Найдем остатки регрессии (т.е. очищаем признак от тренда)

Нарисуем график остатков

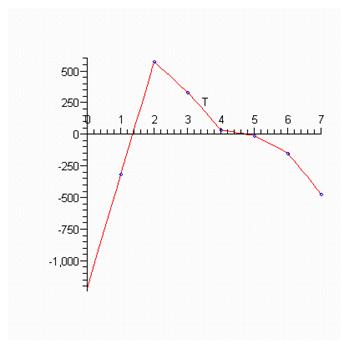
Среднее абсолютное отклонение от тренда равно

Амплитуда колебаний есть разность максимального и минимального отклонения и показывает максимальный разброс отклонений.

Прогноз

Точечный прогноз для

Интервальный прогноз с вероятностью 95%

Выводы. Гиперболическая регрессия оказалась незначима, следовательно обладает плохими прогнозными свойствами.