Действительно, функция F(x)—f(x) не отрицательна, так что

- = ³ 0.

Теорема 6. Если функция f(x) измерима и ограничена на измеримом множестве E, то

£

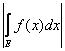4. Предельный переход под знаком интеграла

Здесь мы рассмотрим следующий вопрос: пусть на измеримом множестве E задана последовательность измеримых ограниченных функций

f1(x), f2(x), f3(x), ¼ , fn(x), ¼

которая в каком-нибудь смысле (везде, почти везде, по мере) схо­дится к измеримой ограниченной функции F(x). Спрашивается, будет ли справедливо соотношение

= (1)

Если (1) верно, то говорят, что допустим предельный переход под знаком интеграла.

Легко видеть, что, вообще говоря, это не так. Например, если функции fn(x) определены в сегменте [0, 1] следующим образом:

n при xÎ ,

fn(x) =

0 при x ,

то при всяком x Î [0, 1] будет

fn(x) = 0, но = 1,

и этот интеграл не стремится к нулю.

Поэтому естественно поставить вопрос о тех дополнительных ограничениях, которые нужно наложить на функцию fn(x), чтобы равенство (1) все же имело место.

Мы ограничимся доказательством следующей теоремы.

Теорема (А. Лебег). Пусть на измеримом множестве Е за­дана последовательность f1(x), f2(x), f3(x), ¼ измеримых огра­ниченных функций, сходящаяся по мере к измеримой ограниченной функции F(х)

fn(x) Þ F(x).

Если существует постоянная К, такая, что при всех п и лри всех х

< K,

то

= (1)

Доказательство. Прежде всего заметим, что почти для всех х Î Е будет

£ K. (2)

В самом деле, из последовательности {fn(x)} можно (на основании теоремы Рисса) извлечь частичную последовательность {(x)}, которая сходится к F(x) почти везде. Во всех точках, где

(x) ® F(x),

можно перейти к пределу в неравенстве < K, что и при­водит к (2).

Пусть теперь s есть положительное число. Положим,

An(s) = E()³s), Bn(s) = E()<s.

Тогда

£ = + .

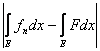В силу неравенства £ + , почти для всех х из множества An(s) будет

< 2K,

так что по теореме о среднем

£ 2K× mAn(s) (3)

(то обстоятельство, что неравенство < 2К может не выпол­няться на множестве меры 0, несущественно. Можно, например, функцию на этом множестве изменить, сделав ее равной нулю; тогда неравенство (3) будет выполняться во всех точках А. Но так как изменение функции на множестве меры 0 не влияет на величину интеграла, то (3) верно и без такого изменения).

С другой стороны, опять-таки в силу теоремы о среднем,

£ smBn(s) £ smE.

Сопоставляя это с (3), находим, что

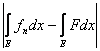£ 2K× mAn(s) + smE. (4)

Заметив это, возьмем произвольное e > 0 и найдем столь малое s > 0, что

s× mE < .

Фиксировав это s, мы, на основании самого определения сходи­мости по мере, будем иметь, что при n ® ¥

mAn(s) ® 0

и, стало быть, для n > N окажется

2K× mAn(s) < .

Для этих n неравенство (4) примет вид

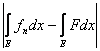< e,

что и доказывает теорему.

Легко понять, что теорема остается верной и в том случае, когда неравенство

< K

выполняется только почти везде на множестве Е. Доказательство остается прежним.

Далее, поскольку сходимость по мере общее обычной сходи­мости, то теорема и подавно сохраняет силу для того случая, когда

fn(x) ® F(x)

почти везде (и тем более везде).

5. Сравнение интегралов Римана и Лебега

Пусть на сегменте [а, b] задана (не обязательно конечная) функ­ция f(х). Пусть

x0 Î [a, b] и d > 0. Обозначим через md(x0) и Мd(х0) соответственно точную нижнюю и точную верхнюю границы функ­ции f(x) на интервале (х0 - d, x0 + d)

md(x0) = inf{f(x)}, Md(x0) = sup{f(x)} (х0 - d < x < x0 + d).

(Само собою разумеется, что мы принимаем во внимание лишь те точки интервала

(х0 - d, x0 + d), которые лежат также и на сег­менте [а, b].)

Очевидно,

md(x0) £ f(x0) £ Md(x0).

Если d уменьшается, то md(x0) не убывает, a Md(x0) не возра­стает. Поэтому существуют определенные пределы

m(x0) = md(x0), Md(x0) = Md(x0),

причем, очевидно,

md(x0) £ m(x0) £ f(x0) £ M(x0) £ Md(x0).

Определение. Функции т(х) и М(х) называются соответственно нижней и верхней функциями Бэра для функции f(x).