Теорема 1 (Р. Бэр). Пусть функция f(х) конечна в точке х0. Для того чтобы f(x) была в этой точке непрерывна, необходимо и достаточно, чтобы было

m(x0) = M(x0). (*)

Доказательство. Допустим, что функция f(х) непрерывна в точке x0. Взяв произвольное e > 0, найдем такое d > 0, что как только

< d,

так сейчас же

< e.

Иначе говоря, для всех х Î (х0 - d, x0 + d) будет

f(x0) - e < f(x) < f(x0) + e.

Но отсюда следует, что

f(x0) - e £ md(x0) £ Md(x0) £ f(x0) + e,

а стало быть, и тем более

f(x0) - e £ m(x0) £ M(x0) £ f(x0) + e,

откуда, ввиду произвольности e, и вытекает (*). Итак, необходимость условия (*) доказана.

Пусть теперь, обратно, дано, что (*) выполнено. Тогда, оче­видно,

m(x0) = M(x0) = f(x0)

и общее значение функций Бэра в точке x0 конечно.

Возьмем произвольное e > 0 и найдем столь малое d > 0, что

m(x0) - e < md(x0) £ m(x0), M(x0) £ Md(x0) < M(x0) + e.

Эти неравенства означают, что

f(x0) - e < md(x0), Md(x0) < f(x0) + e.

Если теперь x Î (х0 - d, x0 + d), то f(x) лежит между md(x0) и Md(x0), так что

f(x0) - e < f(x) < f(x0) + e.

Иначе говоря, из того, что < d вытекает, что

< e,

т. е. функция f(x) непрерывна в точке х0.

Основная лемма. Рассмотрим последовательность дроблений сегмента [а, b]

a = < < ¼ < = b

. . . . . . . . . . . . . . . . . . . . . . . .

a = < < ¼ < = b

. . . . . . . . . . . . . . . . . . . . . . . .

причем при i ® ¥

li = max[-] ® 0.

Пусть есть точная нижняя граница значений функции f(x) на сегменте

[, ]. Введем функцию ji(x), полагая

ji(x) = при x Î (, )

ji(x) = 0 при x = , , ¼ , .

Если х0 не совпадает ни с одной точкой (I = 1, 2, 3, ¼ ; k = 0, 1, 2, ¼ , ni), то

ji(x0) = m(x0).

Доказательство. Фиксируем какое-нибудь i и назовем че­рез [, ] тот из сегментов i-го способа дробления, который содержит точку х0. Так как х0 не совпадает ни с одной из точек деления, то

< x0 <

и, следовательно, при достаточно малых d > 0 будет

(х0 - d, x0 + d) Ì [, ],

откуда следует, что

£ md(x0)

или, что то же самое, что

ji(x0) £ md(x0).

Устремив d к нулю и перейдя к пределу, находим, что при лю­бом i

ji(x0) £ m(x0).

Этим самым лемма уже доказана для случая т(х0) = - ¥. Пусть т(х0) > - ¥ и пусть

h < m(x0).

Тогда найдется такое d > 0, что md(x0) > h.

Фиксировав это d, найдем столь большое i0, что при i > i0 будет

[, ] Ì (х0 - d, x0 + d),

где, как и выше, [, ] есть сегмент, содержащий точку х0. Существование такого i0 следует из условия li ® 0.

Для таких i будет

³ md(x0) > h,

или, что то же самое,

ji(x0) > h.

Итак, для всякого h < m(x0) найдется такое i0, что при i > i0

h < ji(x0) £ m(x0),

а это и значит, что ji(x0) ® m(x0). Лемма доказана.

Следствие 1. Функции Бэра т(х) и М(х) измеримы.

В самом деле, множество точек деления {} счетно и, стало быть, имеет меру нуль. Поэтому лемма означает, что ji(x) ® m(x) почти везде.

Но ji(x) измерима, ибо это ступенчатая функция, значит изме­рима я функция т(x). Для верхней функции Бэра М(х) рассужде­ние аналогично.

Следствие 2. Если в условиях леммы исходная функция f(x) ограничена, то

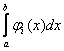(L) ® (L) .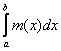

Действительно, если £ K, то, очевидно,

£ K, £ K,

откуда прежде всего следует, что эти функции интегрируемы (L), после чего остается сослаться на теорему Лебега о предельном пе­реходе под знаком интеграла.

Перефразируем теперь следствие 2. Для этого заметим, что

(L) 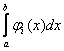= = 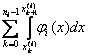= si,

где si есть нижняя сумма Дарбу, отвечающая i-му способу дробле­ния. Таким образом, следствие 2 означает, что при i ® ¥

si ® (L) .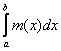

Аналогично можно установить, что верхняя сумма Дарбу Si при возрастании i стремится к интегралу от верхней функции Бэра