Лекции по автоматике 2Рефераты >> Радиоэлектроника >> Лекции по автоматике 2
3. ЛЧХ контура с отрицательной обратной связью.
3.1. Аналитический метод построения ЛЧХ контура с единой ООС.
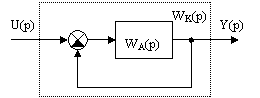
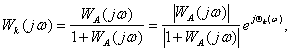 отсюда
отсюда
![]()
![]()
3.2. Построение ЛЧХ контура по номограмм замыкания (Никольса).
Пусть амплитудно-фазовая частотная функция замкнутой системы имеет вид
(1) ![]() причем
причем ![]()
![]()
Амплитудную и фазовую частотные функции замкнутой системы Аз(w) и jз(w) можно выразить через А(w) и j(w) разомкнутой цепи.
Согласно формуле (1) имеем ![]() или, взяв обратные величины слева и справа, получим новое равенство
или, взяв обратные величины слева и справа, получим новое равенство ![]()
Подставим сюда ![]() и приравняем, затем отдельно вещественные и мнимые части. Получим два равенства
и приравняем, затем отдельно вещественные и мнимые части. Получим два равенства ![]()
Сложив сначала квадраты этих выражений, а затем поделив одно из них на другое, получим искомый результат
![]()
![]()
Чтобы не иметь дело на практике с этими формулами, составлены НОМОГРАММЫ замыкания.
 |
Отложив на осях абсцисс и ординат заданные значения j(w) и 20lgА находим значение 20lgАз(w) и jз(w) на поле номограммы в точке с этим координатами. Таким образом, по точкам строится вся частотная характеристика замкнутой системы.
По LA(w) и QA(w) определяются Lk(w) и Qk(w).
При ½WA(jw)½>>1 ½Wk(jw)½»1; а при ½WA(jw)½<<1 Wk(jw)»WA(jw), Lk(w)»WA(w) и Qk(w)»QA(w).
Это значит, что на низких частотах ЛАЧХ замкнутого контура асимптотически стремится к » 0 дБ, а ЛАЧХ к 0 градусов; на высоких частотах Lз(w) асимптотически стремится к высоко частотной асимптоте L(w), а Qр»Qз.
Если контур с неединичной ООС, то его преобразовать к контуру с единичной ООС. Тогда ЛЧХ замкнутой системы строится в два приёма:
![]() вначале стоятся ЛЧХ контура с ед. ООС, где WА(jw)=WПК(jw)×WОС(jw), затем строятся ЛЧХ функции
вначале стоятся ЛЧХ контура с ед. ООС, где WА(jw)=WПК(jw)×WОС(jw), затем строятся ЛЧХ функции ![]() и, наконец, результирующие ЛЧХ системы:
и, наконец, результирующие ЛЧХ системы: ![]() и
и ![]()
4. Параллельное соединение звеньев.
Передаточные функции последовательно-параллельные цепи преобразуем следующим образом:
|
Тогда ЛЧХ системы опреднляется по уравнениям:
|
|
LkШ(w) и QkI(w) могут быть построены по номограмме замыкания, используя ЛЧХ динамических звеньев: ![]()
Структурную схему сколь угодно сложного вида можно упростить и построить логарифмические частотные характеристики.
5. Построение вещественной частотной характеристики контура с единичной ООС по номограмме.
 Вещественная частотная характеристика замкнутой системы можно определить по заданным ЛЧХ разомкнутой цепи системы. Для этого подставим выражение
Вещественная частотная характеристика замкнутой системы можно определить по заданным ЛЧХ разомкнутой цепи системы. Для этого подставим выражение ![]() в формулу
в формулу ![]() Получим
Получим
![]() Выделим вещественную часть из этого выражения
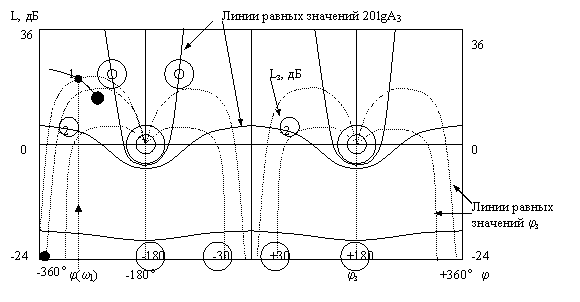
Выделим вещественную часть из этого выражения ![]() По этому выражению построена номограмма
По этому выражению построена номограмма ![]() в плоскости L и Q разомкнутой системы. При L>28 дБ P(w)»1 и при L<-28 дБ P(w)»0. Значение P(w) вблизи точки L=0 и Q = -180° с большей точностью можно определить по специальным таблицам.
в плоскости L и Q разомкнутой системы. При L>28 дБ P(w)»1 и при L<-28 дБ P(w)»0. Значение P(w) вблизи точки L=0 и Q = -180° с большей точностью можно определить по специальным таблицам.
Построены номограммы и для определения ВЧХ замкнутой системы с неединичной ООС Po(w)=F(Lo, Qo).
Пользуются номограммой следующим образом: на поле номограммы отыскивается точка, соответствующая значениям L и Q при выбранной частоте wi, кривая P(w)=const определяет значение P(wi);
если точка расположена между кривыми, то P(wi) определяется путем интерполирования двух ближайших кривых P(w)=const.
Устойчивость САУ.
Первый этап проектирования системы – исследование устойчивости САУ.
Свойство системы приходить в исходное состояние после снятия возмущения называется устойчивостью.
![Подпись: САУ устойчива, если абсолютная величина отклонения регулируемой функции, получившая в результате возмущающего воздействия, по истечении достаточно большого промежутка времени после прекращения действия возмущения становится меньше наперёд заданного значения Е, т.е. lim[Dy(t)]£ Е.](images/referats/4465/image111.gif) Определение.
Определение.
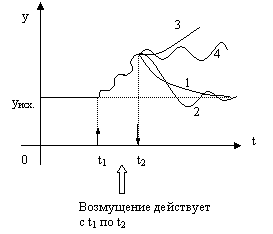 Кривые 1 и 2 характеризуют устойчивую систему, кривые 3 и 4 характеризуют системы неустойчивые.
Кривые 1 и 2 характеризуют устойчивую систему, кривые 3 и 4 характеризуют системы неустойчивые.
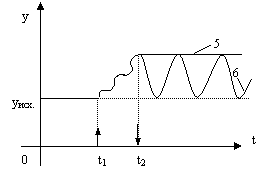
Системы 5 и 6 на границе устойчивости: 5 - нейтральная система, 6 - колебательная граница устойчивости.
Из примеров видно, что различают системы:
1. устойчивые (1,2)
2. неустойчивые (3,4)
3. нейтральные и на грани устойчивости (5,6).
Дифференциальное уравнение САУ в оперативной форме имеет вид:
![]()
Решение дифференциального уравнения (движение системы) состоит из двух частей:
![]()
Система может совершать движения за счёт внешнего воздействия и начальных условий.
За счёт начальных условий – свободное движение, затухающие в устойчивых системах.

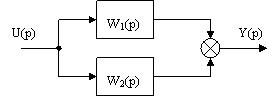
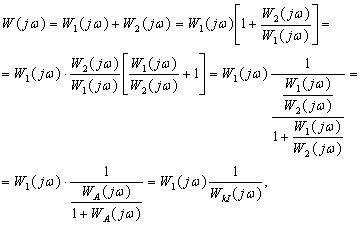 где
где